Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Homotecia en un isósceles
Considere un triángulo $ABC$ con $AB=AC$, y sea $D$ el punto medio de $BC$. La circunferencia de diámetro $AD$ corta el lado $AB$ en $B'$ y el lado $AC$ en $C'$. El circuncírculo de $ABC$, con centro en $O,$ es tangente al lado $AB$ en $P$ y al lado $AC$ en $Q$. Si llamamos $M$ al punto medio de $PQ$, demostrar:
- $B'M$ es paralelo a $BO$
- $M$ es equidistante de los lados del triángulo $AB'C'$
Dos cuerdas por el punto medio de una cuerda
Sea $AB$ una cuerda que no pasa por el centro del círculo y considere dos cuerdas $CD,EF$ que se cortan en el punto medio $P$ de $AB$. Demostrar que si las tangentes a la circunferencia en $C$ y $D$ se cortan en $Q$, y las tangentes en $E$ y $F$ se cortan en $R$, entonces $QR$ es paralela a $AB$.
Criterio para establecer cíclico con potencia de un punto
Si las rectas $AB,CD$ se cortan en $P$ y $PA\cdot{PB}=PC\cdot{PD}$, entonces los puntos $A,B,C,D$ pertenecen a una misma circunferencia. Demostrarlo.
Bisectriz, dos triángulos, circuncírculos, potencia...
La bisectriz del ángulo $B$ del triángulo $ABC$ corta a $CA$ en $D$. El circuncírculo del triángulo $BCD$ corta el lado $AB$ en $E$, y el circuncírculo del triángulo $ABD$ corta al lado $BC$ en $F$. Demostrar que $AE=CF$.
Dos homotecias en un trapecio
Las prolongaciones de los lados $AB$ y $CD$ de un trapecio se intersecan en $K$, y sus diagonales en $L$. Si $M,N$ son los puntos medios de de las bases, demostrar que los puntos $K,L,M,N$ están en una misma recta.
Paralelogramo de baricentros
Las diagonales de un cuadrilátero convexo dividen a éste en cuatro triángulos. Demostrar que sus baricentros forman un paralelogramo.
Transformación geométrica de una circunferencia
Sean dadas dos circunferencias de radios diferentes y una afuera de la otra, y $H$ la intersección de sus tangentes exteriores comunes. Demostrar que para cualquier punto $A$ en una de las circunferencias, existe un punto $B$ en la otra de tal manera que $HA\cdot{HB}=HP\cdot{HQ}$, donde $P,Q$ son los puntos de tangencia de una de las tangentes comunes.
Transformación geométrica de una recta
Sean dadas una circunferencia de radio $r$ y centro $O$, y una recta $l$. Encontrar el lugar geométrico de los puntos $Y$ tales que $OX\cdot OY=r^2$, cuando $X$ se mueve sobre $l$.
Transformación geométrica de un punto
Sean dados una circunferencia de centro $O$ y radio $r$, y un punto $A$ en su interior distinto de $O$. Encontrar un punto $B$ en el plano de tal manera que $OA\cdot{OB}=r^2$. Justifica tu respuesta demostrando la validez del procedimiento que ubica el punto $B$.
Construcción de las simedianas
Considérese el circuncírculo del triángulo $ABC$. Demostrar que si $D$ es la intersección de las tangentes al circuncírculo por $B$ y $C$, entonces $AD$ es el reflejo de la mediana del triángulo por $A$, en el espejo de la bisectriz de $A$.
Antiparalelas
Dos rectas se dicen antiparalelas, respecto a un ángulo de referencia, si forman el mismo ángulo en lados opuestos de la bisectriz de ese ángulo.
Demostrar que:
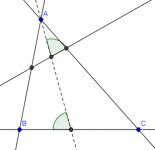
La clave está en la figura
En el triángulo $ABC$, rectángulo en $C$, la bisectriz de $A$ corta a $BC$ en $P$ y la bisectriz de $B$ corta a $CA$ en $Q$. Sean $M$ y $N$ las proyecciones de $P$ y $Q$, respectivamente, sobre el lado $AB$ . Calcular la medida del ángulo $MCN$.
Una propiedad banal de dos isogonales
Sea $ABC$ un triángulo y $\Gamma$ su circuncírculo con centro $O$. La altura de $A$ y el radio $OA$ forman un ángulo cuya medida es la diferencia de las de $B$ y $C$
Circuncentro y ortocentro: una propiedad métrica
Sean $H$ el ortocentro y $O$ el circuncentro del triángulo $ABC$. Si $M$ es el punto medio del lado $BC$, entonces $AH=2MO$. Demostrarlo.
Construcción de un triángulo
Construir el triángulo $ABC$ dadas las longitudes $m_a$ de su mediana desde $A$, $d_a$ de la bisectriz del ángulo $A$, y $h_a$ de la altura del vértice $A$ (respecto a su lado opuesto $BC$).
Isogonales: iso (igual) gono (ángulo)
Demostrar que, en un triángulo $ABC$, la altura de cualquier vértice y la recta que pasa por él y el circuncentro forman el mismo ángulo con la bisectriz (de ese mismo vértice).
Reflejos en el espejo de la bisectiz
Dentro del triángulo $ABC$, considere un punto $P$, y $C'$ y $B'$, los pies de las perpendiculares bajadas desde $P$ a los lados $AB$ y AC, respectivamente. Demostrar que si $Q$ es un punto tal que $C'PB'Q$ es paralelogramo, entonces las rectas $AP$ y $AQ$ son simétricas respecto a la bisectriz del ángulo $A$.
Tres vecinas
A: Al departamento de al lado se acaban de cambiar tres mujeres -según me lo dijo C.
Regla del 41 para ninis
En el país XYZ se aprobó una ley de "jubilación" de ninis (jóvenes que ni estudian ni trabajan). Básicamente, la regla para la "jubilación" es que el joven nini recibirá una pensión estatal de tres salarios mínimos de por vida si sigue siendo joven (menos de 30) y su edad más los años que se ha mantenido nini (sin estudiar ni trabajar) es al menos 41 años. Calcular la edad en que un adolescente de 19 años logrará la pensión si tiene 4 años de nini.
Volumen de una alberca
Una alberca, cuyo espejo del agua es un rectángulo $a\times{b}$, tiene el fondo inclinado también rectangular de manera que la profundidad en un extremo ($h$) es un metro menor que la del otro. Obtener una fórmula para calcular la capacidad de la alberca en metros cúbicos y usarla para $h=1,a=3,b=6$. Nota: puedes suponer que $a,b,h$ están expresadas en metros y las paredes son verticales.
