Intermedio
P4 OMM 1992. Suma de potencias múltiplo de 100
Muestre que $100$ divide a la suma de potencias $$1+11^{11}+111^{111}+\ldots+1111111111^{1111111111}$$
P3 OMM 1992. Siete puntos en hexágono
Considere siete puntos dentro o sobre un hexágono regular y pruebe que
tres de ellos forman un triángulo cuya área es menor o igual que $\frac{1}{6}$ del
área del hexágono.
P2 OMM 1992. Cuartetas y múltiplos de un primo
Sea $p$ un número primo, diga cuántas cuartetas distintas $(a, b, c, d)$ existen, con a, b, c y d enteros y $0 \leq a, b, c, d \leq p-1$, tales que $ad - bc$ sea múltiplo de $p$.
P1 OMM 1992. Tetraedro isósceles
Un tetraedro $OPQR$ es tal que los ángulos $POQ, POR$ y $QOR$ son rectos. Muestre que si $X, Y, Z$ son los puntos medios de $PQ, QR$ y $RP$, respectivamente, entonces el tetraedro $OXYZ$ es isósceles, es decir, tiene sus 4 caras iguales.
P2 OMM 1991. Soldados capicúas
Una compañía de $ n $ soldados es tal que:
- $ n $ es un número capicúa (se lee igual al derecho y al revés, como 15651, 9436349).
- Si los soldados se forman:
--de 3 en 3, quedan 2 soldados en la última fila;
--de 4 en 4, quedan 3 soldados en la última fila;
--de 5 en 5, quedan 5 soldados en la última fila.
a) Hallar el menor $n$ que cumple las condiciones.
b)Demostrar que hay una infinidad de valores $ n $ que las satisfacen.
P1 OMM 1991. Fracciones con denominador 1991
Calcule la suma de todas las fracciones positivas irreducibles (simplificadas)
menores que uno y con denominador es 1991.
P4. OMM 1990. Fichas de dominó
Considere las veintisiete fichas de dominó que quedan quitando la blanca-blanca. Tomando en cuenta los puntos que hay en una ficha, a cada ficha le corresponde un número racional menor o igual que uno. ¿Cuál es la suma de todos estos números?
P3. OMM 1990. ¿Inducción? OK ¿Pero te queda claro qué debes demostrar?
Pruebe que $n^{n-1}-1$ es divisible entre $(n-1)^2$ para todo entero $n\geq2$
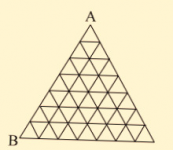
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P4. OMM 1989. Números en expansión decimal
Encuentre el entero positivo mas pequeño $ n $ tal que, si su expansión decimal es $ n=a_ma_{m-1}\ldots{a_2}a_1a_0 $ y $r$ es el número cuya expansión decimal es $r=a_1a_0a_ma_{m-1}\ldots{a_2}0$, entonces $r$ es el doble de $n$.
