Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Mediana a la hipotenusa
Demostrar que, en un triángulo rectángulo, la mediana a la hipotenusa mide la mitad que ésta.
Vértices y ortocentro de un equilátero
Dadas las coordenadas $A=(-\sqrt{3},2), B=(3\sqrt{3},2)$ de dos vértices de un triángulo equilátero $ABC$, y las de su ortocentro $H=(\sqrt{3},0)$, encontrar ls coordenadas del vértice $C$.
Ecuación de la tangente a una circunferencia
Demostrar que la tangente a la circunferencia $x^2+y^2=r$ en el punto $P=(x_1,y_1)$ está dada por la ecuación $xx_1+yy_1=r$
El promedio es el centro
El promedio de dos números reales está exactamente a la mitad del camino entre ellos. Demostrarlo.
La reina ha muerto. ¡Viva la reina!
(Una Gaga (g) en rápido crecimiento, y rompiendo con todos los clichés, ha destronado en 2010 a Madonna (m) --una ex-reyna del pop ya en lento decaimiento.) Dentro de 4 años m tendrá el doble de la edad de g y la diferencia de sus edades es múltiplo de 7. Calcular éstas si se sabe además que g es mayor de edad y m todavía no es adulto en plenitud.
Fan de Lady Gaga
Camila, la princesa de la prepa, se reunió con tres de sus amigas y les regaló copias en CD del album más premiado del año (The Fame Monster, edición de lujo). A la primera le obsequió la mitad de las que traía en su mochila más dos, a la segunda la mitad de los que le quedaban más dos, y a la tercera la mitad de los que le quedaban más dos. Después del reparto le quedó una copia para ella. ¿Cuántas copias de The Fame Monster traía Camila en su mochila?

Línea de Euler
Demuestra que, para un triángulo no equilátero, el circuncentro, el gravicentro y el ortocentro están sobre una misma recta.
Ejercicio con baricentro y circuncentro
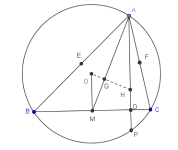
En la figura se muestra un triángulo $ABC$ y su circuncírculo. El segmento que va desde el circuncentro $O$ (concurrencia de mediatrices) al gravicentro $G$ (concurrencia de medianas) se ha prolongado hasta cortar a la altura $AD$ en $H$.
Demostrar:
- (a) Los triángulos $OMG$ y $HAG$ son semejantes
- (b) El segmento $GH$ mide el doble que el $OG$
- (c) En $H$ concurren las tres alturas
Ejercicio con ortocentro
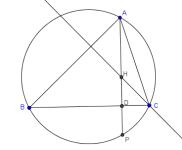
En la figura, $H$ es la intersección de las alturas, y la altura $AD$ del triángulo $ABC$ se ha prolongado hasta cortar el circuncírculo en $P$.
Demostrar:
- (a) El triángulo $HBC$ es isósceles
- (b) La recta $BC$ es mediatriz de $HP$
- (c) Los puntos $H$ y $P$ son simétricos respecto al lado $BC$
Ortocentro, reflexión axial, circuncírculo
Demostrar que, en cualquier triángulo, el punto simétrico del ortocentro respecto a un lado es un punto del circuncírculo.
Divisibilidad entre el producto de tres primos (P6)
Sean $p,q,r$ números primos positivos distintos. Muestra que si $pqr$ divide a $$(pq)^r+(qr)^p+(rp)^q-1$$ entonces $(pqr)^3$ divide a $$3((pq)^r+(qr)^p+(rp)^q-1)$$
Circunferencia por ortocentro y dos vértices de un acutángulo (P5)
Cuadrícula n por 4 (P4)
Sea $n$ un entero positivo. En una cuadrícula $ n\times 4 $, cada renglón es igual a
| 2 | 0 | 1 | 0 |
Un cambio es tomar tres casillas
- consecutivas en el mismo renglón y
- con dígitos distintos escritos en ellas
y cambiar los tres dígitos de estas casillas de la siguiente manera
0 → 1, 1 → 2, 2→0
Dos circunferencias tangentes exteriormente (P3)
Sean $ C_1 $ y $ C_2 $ dos circunferencias tangentes exteriormente en un punto $ A $. Se traza una recta tangente a $ C_1 $ en $ B $ y secante a $ C_2 $ en $ C $ y $ D $; luego se prolonga el segmento $ AB $ hasta intersecar a $ C_2 $ en un punto $ E $. Sea $ F $ el punto medio del arco $ CD $ sobre $ C_2 $ que no contiene a $ E $ y sea $ H $ la intersección de $ BF $ con $ C_2 $. Muestra que $ CD,AF $ y $ EH $ son concurrentes.
Lectura de una tabla
La tabla de la figura muestra las frecuencias del número de puntos que los concursantes de la 24 Olimpiada Mexicana de Matemáticas obtuvieron en cada uno de los 6 problemas del examen nacional.
Cambios de estado de focos en un tablero (P2)
En cada casilla de un tablero $ n\times n $hay un foco. Inicialmente todos los focos están apagados. En un paso, se permite cambiar el estado de todos los focos en una fila o de todos los focos en una columna (los focos prendidos se apagan y los focos apagados se prenden). Muestra que si después de cierta cantidad de pasos hay uno o más focos prendidos entonces en ese momento hay al menos n focos prendidos.
Ternas que cumplen una ecuación (P1)
Encuentra todas las ternas de números naturales $ (a,b,c) $ que cumplan la ecuación $ abc=a+b+c+1 $.
Caracterización de alturas de un acutángulo
En el triángulo acutángulo $ABC$, los puntos $D,E,F$, ubicados respectivamente en los lados $BC,CA,AB$, son tales que $$CD/CE=CA/CB$$ $$AE/AF=AB/AC$$ $$BF/BD=BC/BA$$ Demostrar que $AD,BE,CF$ son alturas.
Huevos en la canasta
Cuántos huevos hay en la canasta si
División feminista
