Combinatoria
P1 OMM 1995. Déjame estrechar tu mano
En una Olimpiada de Matemáticas los concursantes están ocupando todos los asientos de un salón rectangular donde los asientos están alineados en filas y columnas de tal manera que hay más de dos filas y en cada fila hay más de dos asientos. Al inicio del examen un profesor les sugiere que se deseen suerte dándose la mano; cada uno de los concursantes estrecha la mano de los concursantes que están junto a él (adelante, atrás, a los lados y en diagonal) y sólo a éstos. Alguien observa que se dieron 1020 apretones de manos ¿Cuántos concursantes hay?
P6 OMM 1994. Un problema muy negativo
Sea $C$ una cuadrícula de $10x10$. Considere piezas de las siguientes formas:
donde en cada pieza, los cuadrados son de $1 x 1$. Demuestre que:
- 1. $C$ no se puede cubrir completamente con 25 piezas de la forma (a)
- 2. $C$ no se puede cubrir completamente con 25 piezas de la forma (b)
- 3. $C$ no se puede cubrir completamente con 25 piezas de la forma (c)
P4 OMM 1994. Leer primero las páginas primas con 400
Un matemático caprichoso escribe un libro que tiene páginas de la 2 a la 400 y que debe ser leído de la siguiente manera: Primero deberán leerse todas las páginas cuyo número no sea primo relativo con 400 (por suerte, éstas se leen en orden normal, de menor a mayor). Una vez leídas éstas, se toma el último número de las que no se han leído (en este caso 399) y entonces se leen todas las páginas cuyo número no sea primo relativo con él y que no se hayan leído antes.
P2 OMM 1994. Desorden en los números del reloj
Los doce números de un reloj se desprendieron y al colocarlos nuevamente,
se cometieron algunos errores. Demuestre que en la nueva colocación hay
un número que al sumarle los dos números que quedaron a sus lados se
obtiene un resultado mayor o igual a 21.
P3 OMM 1992. Siete puntos en hexágono
Considere siete puntos dentro o sobre un hexágono regular y pruebe que
tres de ellos forman un triángulo cuya área es menor o igual que $\frac{1}{6}$ del
área del hexágono.
P2 OMM 1992. Cuartetas y múltiplos de un primo
Sea $p$ un número primo, diga cuántas cuartetas distintas $(a, b, c, d)$ existen, con a, b, c y d enteros y $0 \leq a, b, c, d \leq p-1$, tales que $ad - bc$ sea múltiplo de $p$.
P1. OMM 1990. Paseos en una cuadrícula
Encuentre el total de caminos que hay del punto $A$ a línea $l$ en la red de la siguiente figura, si en un camino solo está permitido ir hacia la izquierda.
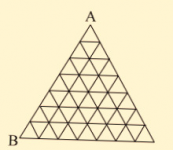
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P7. OMM 1988. Subconjuntos ajenos de {1,2,...,m}
Si $A$ y $B$ son subconjuntos ajenos del conjunto $\{1,2,\ldots,m\}$ y la suma de los elementos de $A$ es igual a la suma de los elementos de $B$, pruebe que el número de elementos de $A$ y también de $B$ es menor que $m/\sqrt{2}$
P4. OMM 1988. Ocho enteros entre uno y ocho
¿Cuántas maneras hay de escoger ocho enteros $a_1,a_2,a_3,\ldots,a_8$ no necesariamente distintos, tales que $1\leq{a_1}\leq\ldots\leq{a_8}\leq8$?
