Problemas - Geometría
Problema 1 - IMO 2016 - Concurrencia de rectas
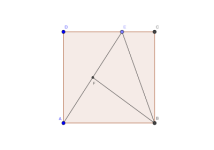
El triángulo $BCF$ tiene ángulo recto en $B$. Sea $A$ el punto en la línea $CF$ tal que $FA = FB$ y $F$ se encuentra entre $A$ y $C$. El punto $D$ está elegido de tal manera que $DA= DC$ y $AC$ es la bisectríz de $\angle DAB$. El punto $E$ es tal que $EA=ED$ y $AD$ es la bisectríz de $\angle EAC$. Sea $M$ el punto medio de $CF$. Sea $X$ el punto tal que $AMXE$ es un paralelogramo (donde $AM \parallel EX$ y $AE \parallel MX$). Demuestra que las líneas $BD$, $FX$ y $ME$ son concurrentes.
Traducido del inglés.
Circunferencia tangente a un cateto
Sea $ABC$ un triángulo rectángulo con $\angle ABC=90$, $BC=72$, $AC=78$. Se considera un punto $D$ sobre el lado $AB$ de tal modo que $2AD=BD$. Sea $O$ el centro de la circunferencia que pasa por los puntos $A$ y $D$ y es tangente al lado $BC$. Encuentra la medida del segmento $OB$.
Medida de segmento para área 2016
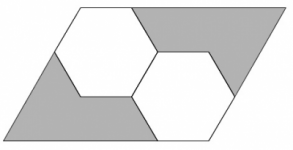
La región complemento de dos hexágonos
En la siguiente figura tenemos dos hexágonos con sus lados iguales. El paralelogramo tiene área de 2016 u2 , ¿cuál es el área de la región sombreada?
Escalinata
Sea $\triangle ABC$ un trinagulo isósceles con $AC=CB, AB=7$ y altura $CD=9$. Los segmentos $a,b,c,d,e,f,g,h$ e $i$ son paralelos a $AB$ y dividen a $CD$ en $9$ segmentos iguales.
Encuentra $a+b+c+d+e+f+i$
El extraño caso del hexágono azul
En un cuadrado $ABCD$ de lado $60$. $E,F,G$ y $H$ son puntos medios de $AB,BC;CD$ y $DA$, respectivamente. Encuentra el área del hexágono $IJKLMN$.
Problema 5. 29a Olimpiada Mexicana de Matemáticas
Sea $I$ el incentro de un triángulo acutángulo $ABC$. La recta $AI$ corta por segunda vez al circuncírculo del triángulo $BIC$ en $E$. Sean $D$ el pie de la altura desde $A$ sobre $BC$ y $J$ la reflexión de $I$ con respecto a $BC$. Muestra que los puntos $D$, $J$ y $E$ son colineales.
Problema 1. 29a Olimpiada Mexicana de Matemáticas
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.
Problema 3(G)
Problema 1 - IMO 2015 - Conjunto de puntos y mediatrices.
Decimos que un conjunto finito $\cal{S}$ de puntos en el plano es equilibrado si para cada dos puntos distintos $A$ y $B$ en $\cal{S}$ hay un punto $C$ en $\cal{S}$ tal que $AC = BC$. Decimos que $\cal{S}$ es libre de centros si para cada tres puntos distintos $A$, $B$, $C$ en $\cal{S}$ no existe ningún punto $P$ en $\cal{S}$ tal que $PA=PB=PC$.
- Demostrar que para todo $n \geq 3$ existe un conjunto de $n$ puntos equilibrado.
- Determinar todos los enteros $n \geq 3$ para los que existe un conjunto de $n$ puntos equilibrado y libre de centros.
