Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Acertijo lógico con tres variables dicotómicas
El exitoso empresario X, rico de nacimiento, quiere contratar los servicios de un guardaespaldas para proteger su persona de la delincuencia organizada. Para ello habla con el director de la agencia Z, especializada en ese tipo de contrataciones.
XXIIIOMM Problema 6
En una fiesta con n personas se sabe que de entre cualesquiera 4 personas, hay 3 de las 4 que se conocen entre sí o hay 3 que no se conocen entre sí. Muestra que las n personas se pueden separar en 2 salones de manera que en un salón todos se conocen entre sí y en el otro salón no hay dos personas que se conozcan entre sí.
XXIIIOMM Problema 5
Considera un triángulo ABC y un punto M sobre el lado BC. Sea P la intersección de las perpendiculares a AB por M y a BC por B, y sea Q la intersección de las perpendiculares a AC por M y a BC por C. Muestra que PQ es perpendicular a AM si y sólo si M es punto medio de BC.
XXIIIOMM Problema 4
Sea $n>1$ un entero impar y sean $a_1,a_2,\ldots,a_n$ números reales distintos. Sea $ M $ el mayor de estos números y sea $m$ el menor de ellos. Muestra que es posible escoger los signos de la expresión $s=\pm {a_1} \pm {a_2}\pm \ldots \pm {a_n}$ de manera que $m<s<M$.
XXIIIOMM Problema 3
Sean $a,b,c$ números reales positivos tales que $abc=1$. Muestra que
$ \frac {a^3}{a^3+2} + \frac {b^3}{b^3+2} + \frac {c^3}{c^3+2}\geq 1$ y que $ \frac {1}{a^3+2} + \frac {1}{b^3+2} + \frac {1}{c^3+2} \leq 1$
XXIIIOMM Problema 2
En cajas marcadas con los números 0,1,2,3,... se van a colocar todos los enteros positivos de acuerdo con las siguientes reglas:
XXIIIOMM Problema 1
Sean ABC un triángulo y AD la altura sobre el lado BC. Tomando a D como centro y a AD como radio, se traza una circunferencia que corta a la recta AB en P, y corta a la recta AC en Q. Muestra que el triángulo AQP es semejante al triángulo ABC.
Un libro de regalo
Fui a la librería y me gustó un libro (Cómo ser feliz en 7 lecciones). Compré varios ejemplares para regalar en Navidad a mis amistades. Por eso la señorita me hizo un descuento de 10 pesos por cada copia. Pagué 1200 pesos. Sin ese descuento, con los 1200 hubiera comprado 4 libros menos.
Construir un cuadrado inscrito a otro
Sean ABCD un cuadrado y M un punto en el interior de éste. Construir con regla y compás un cuadrado PQRS con sus vértices sobre los lados de ABCD y que M esté sobre alguno de los lados de PQRS.
Incentro y circuncírculo
Dado un triángulo $ ABC $, sea $I$ su incentro y $ L $ el punto donde la linea $ AI $ intersecta al circuncirculo . Demuestra que $ AL/LI=(AB+AC)/BC.$
Un problema de lógica
Cuatro miembros de la banda XYZ comían un día juntos en una fonda chiquita. Eran dos mujeres, La Buchona y La Gitana, y dos hombres, El Talibán y El Cochiloco. Cada uno tenía un oficio diferente: Burrero, Gatillero, Guardaespaldas y Oreja. (La mesa era cuadrada y para cuatro.) Con los siguientes datos encontrar el oficio de cada quien.

Un problema de edades
Hace 10 años Jesús tenía la misma edad que Lourdes tiene ahora. Dentro de 7 años Madonna tendrá dos veces la edad de Jesús, aunque actualmente tiene 3 años más que cuatro veces la edad de Lourdes.

Contar clasificando
¿Cuántos triángulos hay en la figura?
IX Olimpiada Norestense de Matemáticas (Problema 3)
El incírculo del triángulo $\triangle ABC$ es tangente al lado $AB$ en el punto $P$ y al lado $ BC $ en el punto $Q$. El círculo que pasa por los puntos $A,P,Q$ corta por segunda vez a la recta $ BC $ en $ M $ y el círculo que pasa por los puntos $C,P,Q$ corta por segunda vez a la recta $ AB $ en el punto $ N $.
Eliminación con dos operaciones
En cada cuadrado de un tablero rectangular hay un entero positivo. Se pueden modificar los números del tablero usando alguno de los siguientes movimientos.
--Multiplicar por 2 cada número de un renglón.
--Restar 1 a cada número de una columna.
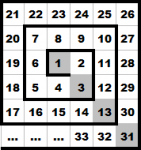
Números en espiral
Considera la sucesión $\{1,3,13,31,\ldots\}$ que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 6)
Alrededor de una circunferencia se marcan 6000 puntos y cada uno se colorea con uno de 10 colores dados, de manera tal que entre cualesquiera 100 puntos consecutivos siempre figuran los 10 colores. Hallar el menor valor k con la siguiente propiedad: Para toda coloración de este tipo existen $k $ puntos consecutivos entre los cuales figuran los 10 colores.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 5)
La sucesión $a_n$ está definida por
$a_1=1, a_{2k}=1+a_k$ y $a_{2k+1}=\frac{1}{a_{2k}}$, para todo entero $k\geq 1$.
Demostrar que todo número racional positivo aparece exactamente una vez en esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea $ ABC $ un triángulo con $AB\neq AC$. Sean $ I $ el incentro de $ ABC $ y $ P $ el otro punto de intersección de la bisectriz exterior del ángulo $A $ con el circuncírculo de $ ABC $. La recta $PI$ intersecta por segunda vez al circuncírculo de $ ABC $ en el punto $J $. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$, con el mismo radio, que se cortan en $A $ y en $ B $. Sea $P $ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C $, la recta $CB$ corta a $C_2$ en $D $ y la bisectriz del $\angle CAD$ intersecta a $C_1$ en $E $ y a $C_2$ en $L $. Sea $F $ el punto simétrico a $D $ con respecto al punto medio de $PE$. Demostrar que existe un punto $X $ que satisface $\angle XFL = \angle XDC = 30^\circ$ y $CX = O_1O_2$.
