Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Ternas Pitagóricas (parte 3)
Demostrar que en cualquier terna pitagórica primitiva $a^2+b^2=c^2$, exactamente dos de los números $a, b, c$ son impares. (Primitiva significa sin divisores en común.)
Ternas Pitagóricas (parte 2)
Demostrar que en cualquier terna pitagórica $a^2+b^2=c^2$, al menos uno de los números a, b, c es divisible entre 5.
Geometría con origami
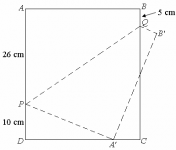
Una hoja de papel en forma rectangular $ABCD$ se dobla a lo largo de la línea $PQ$ de manera que el vértice $A$ quede en el lugar del punto $A’$ y el vértice $B$ en el lugar del punto $B’$. Al medir los segmentos $AP, BQ, DP$, se tiene que miden $26 cm, 5 cm$ y $10 cm$, respectivamente.
¿Cuál es el área del la hoja de papel?
Problema 6, ONMAS 5 (modificado)
En un rectángulo de base 10 y altura 8, se ha inscrito un paralelogramo de tal manera que en las esquinas del rectángulo se forman triángulos de catetos 4 y 7 y 3 y 4. Encuentra la distancia entre los lados opuestos del paralelogramo inscrito en el rectángulo.
Problema 6 OMM 2003
Dado un entero $n$ un cambio sensato consiste en sustituir $n$ por $2n+1$ ó $3n+2$. Dos enteros positivos $a$ y $b$ se llaman compatibles si existe un entero que se puede obtener haciendo uno o más cambios sensatos, tanto a partir de $a$, como a partir de $b$. Encuentra todos los enteros positivos compatibles con $2003$ menores que $2003$.
Problema 4 OMM 2003
Sea $ABCD$ un trapecio con $AB$ paralelo a $DC$. Se toman puntos $P$ y $Q$ sobre $AB$ y $CD$ respectivamente, tales que $\frac{AP}{PB}= \frac{DQ}{QC}$. Sea $M$ la intersección de $AQ$ con $DP$ y sea $N$ la intersección de $PC$ con $QB$. Pruebe que la longitud de $MN$ depende sólo de las longitudes de $AB$ y $DC$ y calcula su valor.
Ciencias blandas (Soft science)
Tres licenciados en ciencias blandas han tenido que entrar al mercado laboral con sus habilidades preuniversitarias. Con la siguiente información decide en qué trabaja cada uno.
Triángulos de igual área
Demostrar que un cuadrilátero es paralelogramo si y sólo si cada una de sus diagonales lo divide en dos triángulos de igual área.
Problema 5, ONMAS 2007
Sean $a, b$ dos enteros tales que $2007 a = 7002b$. Demostrar que $a+b$ no es primo.
Pícaro y caballero (segunda parte)
La Prepa El Pícaro Caballero (de un país muy lejano) tiene dos tipos de profesores: pícaros y caballeros.
Pícaro y caballero
La prepa El Pícaro Caballero (de un país muy lejano) tiene dos tipos de profesores: pícaros y caballeros.
Problema 2 OMM 2003
Sean $A$, $B$ y $C$ tres puntos colineales con $B$ entre $A$ y $C$. Sea $Y$ una circunferencia tangente a $AC$ en $B$, y sean $X$ y $Z$ las circunferencias de diámetros $AB$ y $BC$,
respectivamente. Sea $P$ el otro punto (además de $B$) en el que se cortan las circunferencias $X$ y $Y$; sea $Q$ el otro punto (además de $B$) en el que se cortan las circunferencias $Y$ y $Z$.
Supón que la recta $PQ$ corta a $X$ en un punto $R$ distinto de $P$, y que esa misma recta $PQ$ corta a $Z$ en un punto $S$ distinto de $Q$. Demuestra que concurren $AR$,$CS$, y la tangente
común a $X$ y $Z$ por $B$.
Problema 5 OMM 2003
Problema 5. Se escriben en tarjetas todas las parejas de enteros $(a,b)$ con $1\leq a\leq b \leq 2003$. Dos personas juegan con las tarjetas como sigue: cada jugador en su turno elige $(a,b)$ (que se retira del juego) y escribe el producto ab en el pizarrón (ambos jugadores usan el mismo pizarrón). Pierde el jugador que ocasione que el máximo común divisor de los números escritos hasta ese momento sea $1$. ¿Quién tiene la estrategia ganadora? (Es decir, ¿cuál de los dos jugadores puede inventar un método que asegure su tirunfo?)
Problema 3 OMM 2003
Problema 3. En una fiesta hay el mismo número n de muchachos que de muchachas. Supón que a cada muchacha le gustan a muchachos y que a cada muchacho le gustan b muchachas. ¿Para qué valores de $a$ y $b$ es correcto afirmar que forzosamente hay un muchacho y una muchacha que se gustan mutuamente?
Cálculo inteligente
¿Cuál es el resultado de la siguiente operación?
$(12, 345, 678)^2 - (12, 345, 677) \times (12, 345, 679)$
Método 2 loci (dos lugares) --segunda parte
Trazar una circunferencia que pase por los tres vértices de un triángulo ABC.
Método 2 loci (dos lugares)
Trazar una circunferencia que sea tangente a los tres lados de un triángulo.
Problema 1 OMM 2003
Problema 1. Dado un número $k$ de dos o más cifras, se forma otro
entero $m$ insertando un cero entre las cifras de las unidades y
de las decenas de $k$. Encuentra todos los números $k$ para los
cuales $m$ resulta ser un múltiplo de $k$.
Cuadrados en cada lado y concurrencia.
Sobre los lados del triángulo ABC se han dibujado los cuadrados $ \mathcal{C}_A $, $ \mathcal{C}_B $ y $ \mathcal{C}_C $, de tal manera que un lado del cuadrado es un lado del triángulo y el cuadrado no traslapa al triángulo. El cuadrado $ \mathcal{C}_A $ se encuentra sobre BC; $ \mathcal{C}_B $ sobre AC; y $ \mathcal{C}_C $ sobre AB.
Problema de cíclicos
En un triángulo acutángulo, el círculo de diámetro AB intersecta la altura CE y su extensión en M y N, y el círculo de diámetro AC intersecta la altura BD y su extensión en P y Q. Probar que los puntos M, N, P, Q están sobre una misma circunferencia.
(Nota:Este problema es una extensión del problema dos segmentos iguales.)
