Geometría
Es punto medio si y sólo si el otro es punto medio (OMM 2021 P2)
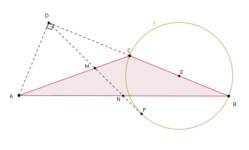
Sea $ABC$ un triángulo tal que $\angle ACB > 90^\circ$ y sea $D$ el punto de la recta $BC$ tal que $AD$ es perpendicular a $BC$. Considere $\Gamma$ la circunferencia de diámetro $BC$. Una recta que pasa por $D$ es tangente a la circunferencia $\Gamma$ en $P$, corta al lado $AC$ en $M$ (quedando $M$ entre $A$ y $C$) y corta al lado $AB$ en $N$.
Demuestra que $M$ es punto medio de $DP$ si, y sólo si $N$ es punto medio de $AB$.
Demostrar que es equilatero
Sea ABCD un cuadrado.
Se construyen 2 triangulos equilatero hacia afuera, CDE y BCF, se trazan las circunferencia con centro en E y con Centro en F que pasan por CD y BC respectivamente.
Sea P la interseccion de las circunferencias.
Demuestra que el trianguo PDB es equilatero.
Tangentes si y sólo si perpendiculares
Sea $ABCD$ un cuadrilátero inscrito en una circunferencia, $l_1$ la recta paralela a $BC$ que pasa por $A$ y $l_2$ la recta paralela a $AD$ que pasa por $B$. La recta $DC$ corta a $l_1$ y $l_2$ en los puntos $E$ y $F$, respectivamente. La recta perpendicular a $l_1$ que pasa por $A$ corta a $BC$ en $P$ y la recta perpendicular a $l_2$ por $B$ corta a $AD$ en $Q$. Sean $\Gamma_1$ y $\Gamma_2$ las circunferencias que pasan por los vértices de los triángulos $ADE$ y $BFC$, respectivamente. Demuestra que $\Gamma_1$ y $\Gamma_2$ son tangentes si y sólo si $DP$ es perpendicular a $CQ$.
Circunferencias con relación de radios
Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ dos circunferencias tangentes externamente en $S$ tales que el radio de $\mathcal{C}_2$ es el triple del radio de $\mathcal{C}_1$. Sea $l$ una recta que es tangente a $\mathcal{C}_1$ en $P$ y tangente a $\mathcal{C}_2$ en $Q$, con $P$ y $Q$ distintos de $S$. Sea $T$ el punto en $\mathcal{C}_2$ tal que $TQ$ es diámetro de $\mathcal{C}_2$ y sea $R$ la intersección de la bisectriz de $\angle SQT$ con el segmento $ST$. Demuestra que $QR = RT$
Punto exterior a un cuadrado
Sea $ABCD$ un cuadrado. P un punto sobre la semicircunferencia de diámetro AB exterior al cuadrado. Sean M y N las intersecciones de PD y PC con AB, respectivamente. Demuestra que $MN^2 = AM \cdot BN$
Cíclico dentro de un isóceles
Sea $ABC$ un triángulo con $AB=AC$ de gravicentro $G$. $M$ y $N$ los puntos medios de $AB$ y $AC$ respectivamente y $O$ el circuncentro del trángulo $BCN$. Muestra que $MBOG$ es un cuadrilátero cíclico.
Geometría del Primer Selectivo 2016
Sea $ABCD$ un cuadrilátero cíclico y $E$ y $F$ puntos sobre la recta $AB$ pero fuera del segmento $AB$ con $A$ entre $E$ y $B$ y $B$ entre $A$ y $F$. Demuestra que si $\angle BED = \angle AFC = \angle DAC$ entonces $EA=BF$.
Problema 3 - IMO 2016 - Área de un polígono cíclico de coordenadas enteras.
Sea $P=A_1A_2 \dots A_k$ un polígono convexo en el plano. Los vértices $A_1, A_2, \dots, A_k $ tienen coordenadas enteras y están sobre un círculo. Sea $\mathcal{S}$ el área de $P$. Los cuadrados de las los lados de $P$ son todos divisibles por un entero dado $n$. Demuestra que $2\mathcal{S}$ es divisible por $n$,
Traducido del inglés.
Problema 1 - IMO 2016 - Concurrencia de rectas
El triángulo $BCF$ tiene ángulo recto en $B$. Sea $A$ el punto en la línea $CF$ tal que $FA = FB$ y $F$ se encuentra entre $A$ y $C$. El punto $D$ está elegido de tal manera que $DA= DC$ y $AC$ es la bisectríz de $\angle DAB$. El punto $E$ es tal que $EA=ED$ y $AD$ es la bisectríz de $\angle EAC$. Sea $M$ el punto medio de $CF$. Sea $X$ el punto tal que $AMXE$ es un paralelogramo (donde $AM \parallel EX$ y $AE \parallel MX$). Demuestra que las líneas $BD$, $FX$ y $ME$ son concurrentes.
Traducido del inglés.
Circunferencia tangente a un cateto
Sea $ABC$ un triángulo rectángulo con $\angle ABC=90$, $BC=72$, $AC=78$. Se considera un punto $D$ sobre el lado $AB$ de tal modo que $2AD=BD$. Sea $O$ el centro de la circunferencia que pasa por los puntos $A$ y $D$ y es tangente al lado $BC$. Encuentra la medida del segmento $OB$.
