Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Ecuación de suma de fracciones
Razonado con suma de dígitos
Mauricio ya cumplió años en el 2010. Al sumar los dígitos de la fecha de su nacimiento se dio cuenta que obtenía su edad. ¿Cuántos años puede tener Mauricio?
Seccionado de un cubo de lado $3$
Un cubo de lado 3 se divide en 27 cubitos unitarios. ¿De cuántas formas podemos elegir tres cubitos de manera que sus centros estén en una misma recta? Nota: El centro de un cubito se localiza en el punto medio de una diagonal mayor.
Demostrar perpendicular
Sean $ABC$ un triángulo rectángulo y $M$ el punto medio de la hipotenusa $BC$. Sus catetos cumplen que $CA$ es menor que $AB$. Se coloca un punto $D$ sobre $AB$ de manera que $CA = AD$. Finalmente, sea $E$ el punto común de $AM$ y $CD$. Si $F$ es un punto sobre $BC$ tal que $EF$ es paralela a BC $AC$, demostrar que $AM$ es perpendicular a $FD$.
Tangentes a circunferencia desde el centro de otra
Considere las circunferencias $a$ y $b$ de centros $A$ y $B$ respectivamente. Desde el centro $A$ se trazan las tangentes a $b$ y éstas cortan a $a$ en los puntos $P$ y $Q$. Desde el centro $B$ se trazan las tangentes a $a$ que cortan a $b$ en $R$ y $S$. Demostrar que $PQRS$ es un rectángulo.
Número igual a la suma del factorial de sus dígitos
Encontrar todos los números de 3 dígitos de la forma $abc$ ($a$ es el dígito de las centenas, $b$ es el dígito de las decenas y $c$ es el dígito de las unidades) que cumplan con: $abc = a!+b!+c!.$ (Nota: n! es el producto n(n-1)...(2)(1) y se lee $n$ factorial.)
Sumas de productos de filas y columnas en un tablero
En un tablero de 2009 x 2009 cuadritos, se han llenado todos los cuadritos usando solamente 1 o -1, y se ha obtenido el producto de los números de cada fila y de cada columna. Encontrar todas las posibles sumas de estos 4018 productos.
Ejemplo: en un tablero de 3x3 un posible llenado es:
1 1 1
1 1 -1
1 1 1
y la suma de los 6 productos 1 + 1 -1 +1 -1 +1 = 2
Elección condicionada de 3
¿De cuántas maneras se pueden escoger 3 números diferentes del conjunto $C=\{1,2,3,...,19,20\}$ de manera que la suma de esos tres números sea múltiplo de 3?
Círculo de diámetro la base de un triángulo
Sea $ABC$ un triángulo tal que la circunferencia $S$ de diámetro $BC$ pasa por el punto medio $M$ de $AB$. Sea $N$ un punto sobre $S$ de manera que $MN$ es diámetro de $S$. Probar que el área del triángulo $ABC$ entre el área del triángulo $MNC$ es 2.
Razón de áreas
En el rectángulo $ABCD$, los puntos $P, Q, R, S$, uno en cada lado, dividen el lado donde están en razón 3:2. ¿Cuál es el cociente del área del paralelogramo $PQRS$ entre el área de la región del rectángulo que queda afuera del paralelogramo? (N del E: en el examen se dio la figura.)
Minimizar invitaciones
En el Messenger (MSN), para que dos personas estén en contacto, es suficiente con que una de ellas envíe una invitacíon a la otra y ésta la acepte. Luis tiene 114 amigos de la ONMAS 2009, y ninguno de ellos se tiene agregado al Messenger entre sí. Luis les propone a ellos la idea de ponerse en contacto. ¿Cuál es el número mínimo de invitaciones aceptadas para que Luis y todos sus amigos estén en contacto por el MSN?
Demostrar paralelogramo
Sean $ABCD$ un paralelogramo, y $P, Q, R, S$ puntos exteriores a él. $M_1$ y $M_2$ son puntos medios de $PA$ y $AQ$, respectivamente, y $G_1$ la intersección de $QM_1$ y $PM_2$. ($G_1$ es el gravicentro del triángulo $PAQ$). De la misma manera se localizan los puntos $G_2, G_3, G_4$ en los triángulos $QRB, RSC$ y $SPD$, respectivamente. Demuestre que $G_1G_2G_3G_4$ es un paralelogramo.
Pesas y pesadas
Se tiene una balanza de dos platillos y un número $n$ de piezas de idéntica apariencia, pero una de ellas tiene un peso mayor al de las demás. ¿Cuál debe ser el valor máximo de $n$ para encontrar la pieza de peso diferente en a lo más cuatro pesadas?
Dos listas de números
Juan tiene la lista de todos los números de 8 dígitos que se pueden formar con cuatro 1’s y cuatro 2’s. José tiene la lista de todos los números de cuatro dígitos que se pueden formar con los dígitos 1, 2, 3 y 4 y que tengan la misma cantidad de 1’s que de 2’s. Por ejemplo: 1234, 3343, 1122, etc. ¿Quién tiene más números en su lista?
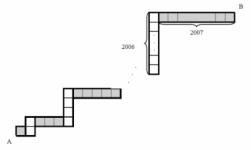
2007 ONMAS escalera
Tengo 2007 rectángulos de dimensiones $1\times1, 1\times2, 1\times3,…, 1\times2007$ y los coloco en ese orden poniendo uno horizontal, luego otro vertical, etc. (como se muestra en la figura) formando una escalera.
¿Cuánto mide el segmento que va desde el punto A hasta el punto B?
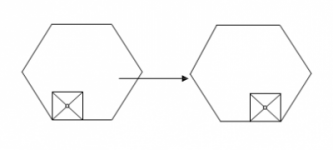
Cuadrado deslizante en hexágono
En la esquina inferior izquierda de un hexágono regular de lado 4 metros se coloca un cuadrado de lado 2 metros, tal y como se observa en la parte izquierda de la figura.
El cuadrado “rueda” (sin deslizarse) sobre los lados del hexágono y por la parte interior de éste, girando en el sentido inverso de las agujas del reloj y manteniendo siempre un vértice apoyado en un lado del hexágono (el primer movimiento aparece en la figura). Cuando el punto $P$ --que es la intersección de las diagonales del cuadrado-- vuelve a su posición inicial ¿Cuántos metros ha recorrido?
Residuo de una serie de potencias
Encontrar el residuo de dividir entre 5 el número $N= 1 + 4 + 4^2 + 4^3 + 4^4 +\ldots+4^{2007}$
Reparto circular con regla añadida
El abuelo reparte 2007 monedas entre sus nueve nietos (digamos A, B, C, D, E, F, G, H e I) de la siguiente manera: Los sienta alrededor de una mesa en el orden de sus nombres y va entregando en ese mismo orden una moneda a cada uno; empieza con A y, al completar la vuelta, la siguiente vuelta comienza con el último, es decir, le entrega una más a I y continúa con A; entregando moneda por moneda, termina la siguiente vuelta con H, le entrega su moneda y con él mismo inicia la siguiente vuelta. Procede de esta manera hasta agotar todas las 2007 monedas. ¿Cuántas monedas le tocaron a cada nieto? ¿A cuál de los nietos le entregó la última moneda?
Un cuadrilátero con muchos segmentos iguales
En un cuadrilátero $ABCD$, con ángulos interiores menores a 180 grados, los lados $AB, BC$ y $CD$ son iguales. También sabemos que $AD = AC = BD$. Encuentra la medida del ángulo $ABC$.
