Problemas
También puedes compartirnos alguno de tus problemas favoritos:
P6 OMM 1992. Muchas preguntas con un rectángulo
Sea $ABCD$ un rectángulo. Sean $I$ el punto medio de $CD$ y $M$ la intersección de $BI$ con la diagonal $AC$.
- 1. Pruebe que $DM$ pasa por el punto medio de $BC$.
-
2. Sea $E$ el punto exterior al rectángulo tal que $ABE$ sea un triángulo
isósceles y rectángulo en $E$. Además, supongamos que $BC = BE = a$.
Pruebe que $ME$ es bisectriz del ángulo $AMB$. - 3. Calcule el área del cuadrilátero $AEBM$ en función de $A$.
P5 OMM 1992. Desigualdad con suma de radicales
Sean $x, y, z$ números reales positivos tales que $x + y + z = 3$. Si
$$S = \sqrt{2x + 3} + \sqrt{2y + 3} + \sqrt{2z + 3},$$
pruebe que $6 < S \leq 3\sqrt{5}$
P4 OMM 1992. Suma de potencias múltiplo de 100
Muestre que $100$ divide a la suma de potencias $$1+11^{11}+111^{111}+\ldots+1111111111^{1111111111}$$
P3 OMM 1992. Siete puntos en hexágono
Considere siete puntos dentro o sobre un hexágono regular y pruebe que
tres de ellos forman un triángulo cuya área es menor o igual que $\frac{1}{6}$ del
área del hexágono.
P2 OMM 1992. Cuartetas y múltiplos de un primo
Sea $p$ un número primo, diga cuántas cuartetas distintas $(a, b, c, d)$ existen, con a, b, c y d enteros y $0 \leq a, b, c, d \leq p-1$, tales que $ad - bc$ sea múltiplo de $p$.
P1 OMM 1992. Tetraedro isósceles
Un tetraedro $OPQR$ es tal que los ángulos $POQ, POR$ y $QOR$ son rectos. Muestre que si $X, Y, Z$ son los puntos medios de $PQ, QR$ y $RP$, respectivamente, entonces el tetraedro $OXYZ$ es isósceles, es decir, tiene sus 4 caras iguales.
P6 OMM 1991. Triángulos en un polígono
En un polígono de $ n $ lados, ($n \geq 4$) se considera una familia $T$ de triángulos, formados con los vértices del polígono, con la propiedad de que cada dos triángulos de la familia cumple alguna de las siguientes dos condiciones:
– No tienen dos vértices en común.
– Tienen dos vértices en común.
Demuestre que $T$ tiene a lo más $ n $ triángulos.
P5 OMM 1991. Suma de cuadrados cuadrado
La suma de los cuadrados de dos números consecutivos puede ser un cuadrado perfecto (por ejemplo $3^2 + 4^2 = 5^2$).
a) Pruebe que la suma de los cuadrados de $m$ enteros consecutivos no puede
ser un cuadrado para $m$ igual a 3 y 6.
b) Encuentre un ejemplo de 11 números consecutivos cuya suma de cuadrados sea un cuadrado perfecto.
P4 OMM 1991. Ocho puntos concíclicos
Considere un cuadrilátero convexo $ABCD$ en el que las diagonales $AC$ y $BD$ se cortan formando ángulo recto. Sean $M, N, R$ y $S$ los puntos medios de los segmentos $AB, BC, CD$ y $AD$, respectivamente. Sean $W,X, Y$ y $Z$ las proyecciones de los puntos $M, N, R$ y $S$ sobre las rectas $DC, AD, AB$ y $BC$, respectivamente. Pruebe que todos los puntos $M, N,R, S, W, X, Y$ y $Z$ están sobre una misma circunferencia.
P3 OMM 1991. Cuatro canicas en una esfera
Se tienen 4 canicas de radio uno colocadas en el espacio de tal manera que
cada una de ellas es tangente a las otras tres. ¿Cuál es el radio de la esfera
más pequeña que contiene a las canicas?
P2 OMM 1991. Soldados capicúas
Una compañía de $ n $ soldados es tal que:
- $ n $ es un número capicúa (se lee igual al derecho y al revés, como 15651, 9436349).
- Si los soldados se forman:
--de 3 en 3, quedan 2 soldados en la última fila;
--de 4 en 4, quedan 3 soldados en la última fila;
--de 5 en 5, quedan 5 soldados en la última fila.
a) Hallar el menor $n$ que cumple las condiciones.
b)Demostrar que hay una infinidad de valores $ n $ que las satisfacen.
P1 OMM 1991. Fracciones con denominador 1991
Calcule la suma de todas las fracciones positivas irreducibles (simplificadas)
menores que uno y con denominador es 1991.
P6. OMM 1990. Una configuración cargada de teoría
Sea $ABC$ un triángulo rectángulo con ángulo recto en $C$. Sea $l$ cualquier recta que pase por $B$ y que corte al lado $AC$ en un punto $E$. Sean $F$ el punto medio de $EC$, $G$ el punto medio de $CB$ y $H$ el pie de la altura de $C$, respecto a $AB$, en el triángulo $ABC$. Si $I$ denota el circuncentro del triángulo $AEH$ (punto de intersección de las mediatrices de los lados), pruebe que los triángulos $IGF$ y $ABC$ son semejantes.
P5. OMM 1990. Baricentro de coordenadas enteras
Si $P_1,P_2,\ldots,P_{19}$ son diecinueve puntos del plano con coordenadas enteras tales que cada tres de ellos son no colineales, demuestre que hay tres con la propiedad de que su baricentro (punto de intersección de las medianas de un triángulo), también tiene coordenadas enteras.
P4. OMM 1990. Fichas de dominó
Considere las veintisiete fichas de dominó que quedan quitando la blanca-blanca. Tomando en cuenta los puntos que hay en una ficha, a cada ficha le corresponde un número racional menor o igual que uno. ¿Cuál es la suma de todos estos números?
P3. OMM 1990. ¿Inducción? OK ¿Pero te queda claro qué debes demostrar?
Pruebe que $n^{n-1}-1$ es divisible entre $(n-1)^2$ para todo entero $n\geq2$
P2. OMM 1990. Relación de inradios
Sea $ABC$ un triángulo rectángulo con ángulo recto en $B$, y $H$ el punto de intersección del lado $AC$ y la altura por $B$. Llamemos $r,r_1,r_2$ a los radios de las circunferencias inscritas en los triángulos $ABC,ABH,HBC$, respectivamente. Encuentre una igualdad que relacione $r,r_1,r_2$.
P1. OMM 1990. Paseos en una cuadrícula
Encuentre el total de caminos que hay del punto $A$ a línea $l$ en la red de la siguiente figura, si en un camino solo está permitido ir hacia la izquierda.
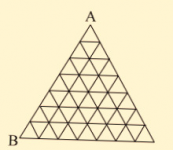
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P5. OMM 1989. Círculos tangentes
Sean $C_1$ y $C_2$ dos círculos tangentes de radio 1 dentro de un círculo $C$ de radio 2. Sea $C_3$ un círculo dentro de $C$ tangente a cada uno de los círculos $C,C_1,C_2$. Sea $C_4$ un círculo dentro de $C$ tangente a $C,C_1,C_3$. Demuestre que los centros de $C,C_1,C_3,C_4$ son los vértices de un rectángulo.
