Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Una diofantina muy difícil
Resolver la ecuación diofantina siguiente para enteros no negativos x,y,z:
$$x^2+y^4+z^6=2^{1111}$$
Inferencias de paridad
Sea $n\geq2$ un entero. Los números $x_1,x_2,\ldots,x_n$ son elementos del conjunto $\{-1,1\}$ y cumplen la ecuación $x_1x_2+x_2x_3+\ldots+x_nx_1=0$. Demostrar que $ n $ es múltiplo de 4.
Adictos al Xbox
Los adolescentes de una preselección olímpica de matemáticas tienen una actividad de entretenimiento favorita: 17 son adictos al Xbox (conjunto A1), 13 a las series americanas de TV (A2), 8 a la resolución de problemas de concurso (A3), y 6 no tienen actividad recreativa conocida.
Pudorosa (segunda parte)
Decidir --con prueba-- si la ecuación diofantina $123x+426y=8$ tiene solución.
Una pudorosa propiedad del máximo común divisor
Si $a, b$ son enteros y cumplen $7a-38b=-2$ ¿qué se puede concluir sobre el máximo común divisor de a y b?
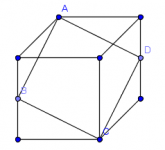
Cuadrilátero en un cubo
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
¿Es múltiplo de 11? (Que lo diga Fermat.)
Decidir --con prueba-- si $61^{61}+71^{71}$ es divisible entre 11.
ExSel2_Pr1: Inclusión y exclusión... pero basta con razonarlo
¿Cuántos números enteros positivos no mayores que 1000 no son ni cuadrados ni cubos?
Elemental,... pero sólo si sabes usar el PTF
Encontrar todos los primos $q$ tales que $4+2^q$ es múltiplo de $2q.$
Progresión aritmética con un cuadrado
Demostrar que si una progresión aritmética de enteros positivos contiene un cuadrado perfecto entonces contiene infinitamente muchos cuadrados perfectos.
Los primos no se factorizan... excepto en la forma 1( p )
Encontrar todos los enteros positivos n tales que $n^{20}+n^{10}+1$ es un primo.
Otro de puros 1´s
Demostrar que todo primo impar n excepto el 5 divide a algun numero de la forma $111...11$ ($k$ digitos, todos unos).
P divide a una sumota
Sea $p$ un número primo. Encontrar la condición que debe cumplir n para que $1+n+n^2+....+n^{p-2}$ es múltiplo de $p$.
Encontrar k...
Determina si existen infinitos enteros $ k $, que cumplen que para cualquier primo $ p $, el numero $p^2+k$ siempre es compuesto.
Por ejemplo si tomamos $k=2$, para $p=2$ dicho numero es compuesto pero para $p=3$ no lo es...
Semicírculo y la descomposición en dos sumandos de un segmento.
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que $BP=PQ+QC$
División en casos
Encontrar todas las tripletas $(p,q,r)$ de números primos tales que $p^q+p^r$ es un cuadrado perfecto.
Criba modular
Encontrar todas las soluciones $(x,y)$ en enteros positivos para la ecuación $7^x-3\cdot 2^y=1.$
Múltiplo de 11 compuesto de unos
Sea $p$ un un entero positivo. El número $11p$ está compuesto de $m$ dígitos todos iguales a 1. Encontrar todos los valores de $m$ para los cuales $p$ es primo.
Áreas enteras de triángulos
El área del triángulo $ ABC $ es un entero. Sobre los lados $ BC$ y $AC$ se eligen los puintos $X$ y $Y$, respectivamente. Los segmentos $AX$ y $ BY$ se cortan en un punto $P$ dentro del triángulo $ ABC $. El área de $BPX$ es 1, la de $APY$ es 2, y la de $APB$ es un entero. Encontrar el área del triángulo $ABC.$
Biblioteca
En mi biblioteca hay 5 libros de álgebra, 6 de combinatoria, y 8 de geometría, y todos son diferentes.
a) ¿De cuántas formas puedo elegir dos?
b) ¿De cuántas formas puedo elegir dos del mismo tema?
c) ¿De cuántas formas puedo elegir dos pero que no sean del mismo tema?
