Problemas
También puedes compartirnos alguno de tus problemas favoritos:
El lugar geométrico de la reflexión de un punto
Sean $ P$ un punto en el interior de una circunferencia $\mathcal{C}$ y $ M$ un punto sobre $\mathcal{C}$. Definamos $ N$ el punto sobre $\mathcal{C}$ tal que el ángulo $\measuredangle MPN = 90^{\circ}$ (en sentido contrario de las manecillas del reloj). Llamemos $P'$ el punto que resulta de reflejar $ P$ con respecto a $MN$.
Construcción de una circunferencia ortogonal
Sea dada una circunferencia $c$. Demostrar que el siguiente procedimiento produce una circunferencia ortogonal a $c$ con centro en un punto $P$ fuera de $c$.
1) Trazamos las tangentes a $c$ desde $P$ ubicando los puntos de tangencia $T$ y $T'$.
2) Trazamos la circunferencia con centro en $P$ y radio $PT$. Esta es la circunferencia ortogonal pedida.
Caracterización del eje radical
Demostrar que el eje radical de dos circunferencias es el lugar geométrico de los puntos que cumplen la propiedad de que el producto de la suma por la diferencia de sus distancias a los centros es una constante.
Valor de la potencia de un punto
Demostrar que la potencia de un punto $P$ respecto a la circunferencia $c$ con centro en $O$ y radio $ r $ es $PO^2-r^2$
Construcción del inverso
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el inverso P' de P con respecto a la circunferencia c.
1) Trazar la recta OP.
2) Trazar una de las tangentes desde P a c, y llamar T al punto de tangencia.
Trazar una tangente a una circunferencia
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el punto de tangencia T de la tangente que pasa por P.
1) Trazar el segmento OP.
2) Trazar la circunferencia de diámetro OP y llamar T a uno de los puntos de intersección con c.
Altura de un triángulo rectángulo
Sea AP la altura de A respecto a la hipotenusa BC del triángulo rectángulo ABC. Demostrar que se cumplen las proporciones PB/BA=BA/BC y BP/PA=PA/PC.
Cuerda común y línea de centros
La línea de centros (recta que pasa por los centros) de dos círculos que se intersectan es mediatriz de su cuerda común.
Cuerda y tangentes comunes
La cuerda común de dos círculos pasa por el punto medio de la tangente común a los círculos. Demostrarlo.
Círculos en dos lados de un triángulo
Tomando como diámetros los lados AB y AC del triángulo ABC, se trazan sendos círculos. Demostrar que su otro punto de intersección (aparte de A) está sobre el lado BC.
Lema de las alturas (para cíclicos)
Cualesquiera dos vértices de un triángulo son concíclicos con los pies de sus alturas.
Problema 5 IMO 2005
Sea $ ABCD$ un cuadrilatero convexo con $ BC=DA $ y además las rectas $ BC,DA $ no son paralelas. Consideremos dos puntos variables $ E,F $ sobre $ BC, DA $ respectivamente, que satisfacen $ BE=DF$ . Sea $P$ la interseccion de $ AC, BD.$ Las rectas $BD$ y $EF$ se intersectan en $Q$ y las rectas $AC$ y $EF$ se intersectan en $R$.
Uno de Ciclicos (tema del 1er entrenamiento 09)
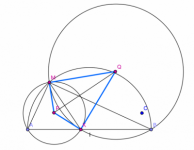
Sea AB diametro de una semicircunferencia. Un punto M sobre la semicircunferencia y K un punto spbre AB. Una circunferencia con centro P pasa por A,M,K, y otra circunferencia de centro Q pasa por M,K,B. Demostrar que MPKQ es un cuadrilatero ciclico.
PROBLEM 1 DE LA CENTRO
Determine el menor entero positivo $ N $ tal que la suma de sus dígitos sea 100 y la suma de $2N$ sea 110
Probar simediana
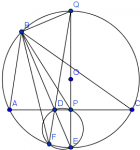
Considera un triangulo $ ABC $ Con $ BD $ su bisectriz interna ( $D$ sobre $AC$) Sea $E$ el punto donde se intersectan $BD$ y el circuncirculo del triangulo $ ABC $. El circulo de diametro $DE$ corta al circuncirculo del triangulo $ ABC $ en los puntos $D,F$ demuestra que $BF$ es la simediana del triangulo $ ABC $
Problema 2 BMO 2009
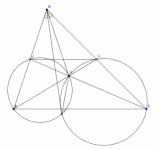
Sea $MN$ una línea paralela al lado $ BC $ del triángulo $ ABC $, con $ M $ sobre el lado $AB$ y $ N $ sobre el lado $AC$. Las íineas $BN$ y $CM$ se intersectan en un punto $P$. Los circuncírculos de los triángulos $BPM$ y $CPN$ se intersectan en $P$ y $Q$. Demostrar que $\angle{BAQ}=\angle{CAP}$
Otro de un cuadrado, dentro de otro cuadrado.
Sea ABCD un cuadrado de centro O. Sean P, Q, R y S puntos en DA, AB, BC y CD, repectivamente, tales que P,O y R son colineales; y Q, O y S también lo son (colineales), y de manera que PR es perpendicular a QS. Demostrar que el cuadrilátero PQRS es un cuadrado.
L1.P23 (Un clásico --para terminar la lista)
Encontrar todas las soluciones en enteros positivos de la ecuación $1/x+1/y+1/z=1.$
L1.P22 (Una ecuación cuadrática)
La ecuación $x^2+bx+2=0$ tiene solamente una raíz. Determinar los valores de $b$.
L1.P21 (Cuadrado en el centro de un cuadrado)
Los puntos medios $L,M,N,O$ de los lados $QR,RS,SP,PQ$ de un cuadrado $PQRS$ se unen con con un segmento de recta a los vértices de éste de manera que se forme un cuadrado $P'Q'R'S'.$ Calcular la razón de áreas de los dos cuadrados.
