Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Doce bolas y tres pesadas
Determinar, con el auxilio de una balanza y en sólo tres pesadas, una bola de entre doce, que pesa distinto a las demás. Además, determinar si la bola pesa más o menos que las otras.
Yoga de leche
Una yoga de 5 litros está llena de leche. Dos botellas vacías de 2 y 3 litros respectivamente están disponibles para transferir el líquido entre las botellas y la yoga de 5 litros. Exhibir un procedimiento para lograr 4 litros de leche en la yoga de 5 litros. Encontrar una sucesión de transferencias de leche de longitud 3.
Las cervezas de Bart Simpson
Bart Simpson cuenta, usando sus dedos de la mano derecha, las cervezas que se ha tomado su papá en la semana. Si cuenta empezando con el meñique y termina en el índice pulgar y vuelve a empezar con el meñique, y contó 777 ¿en qué dedo terminó la cuenta? (Nota: Bart solamente tiene 4 dedos. Además, hay que suponer que sabe contar hasta 777...) ¿En qué dedo terminaría si tuviese 5 dedos?

Fermat converso (en general, espurio)
Demostrar que si $p, q$ son dos primos distintos para los cuales $a^p\equiv a \pmod{q}$ y $a^q\equiv{a} \pmod{p}$, entonces $a^{pq} \equiv a \pmod{pq}$. }
Demostrar, con este resultado, el siguiente contraejemplo para la conversa del pequeño teorema de Fermat: $2^{340} \equiv 1 \pmod{341}$ --¡pero 341 es compuesto!
Una factorización no trivial
Factorizar las siguientes expresiones algebraicas:
$$x^4 +6x^3 +11x^2 +6x +1$$
$$x^4 +6x^3 +11x^2 +6x$$
Genera un problema de concurso, en vista de las dos factorizaciones.
Ángulos en el reloj
¿Cuál es el ángulo que forman las manecillas del reloj a las 9:30? (Argumento fiador requerido.)
Problema 6, XII Olimpiada Iberoamericana
Sea $P=\{P_1, P_2, \dots, P_{1997}\}$ un conjunto de 1997 puntos en el interior de un círculo de radio 1, siendo $P_1$ el centro del círculo. Para cada $k=1, \dots, 1997$ sea $x_k$ la distancia de $P_k$ al punto de $ P$ más próximo a $P_k$ y distinto de $P_k$. Demostrar que:
$$x_1^2 + x_2^2 + \cdots +x_{1997}^2 \leq 9$$
P3. OMM 1993
Dentro de un pentágono de área 1993 se encuentran 995 puntos. Considere estos puntos junto con los vértices del pentágono.
Muestre que, de todos los triángulos que se pueden formar con los 1000 puntos anteriores como vértices, hay al menos uno de área menor o igual que 1.
Partición de un conjunto
Encontrar todos los enteros positivos $ n $ para los cuales el conjunto $A= \{n, n+1, n+2, n+3, n+4, n+5\}$ puede particionarse en dos subconjuntos con el mismo producto de sus miembros (el producto de los números en uno de los subconjuntos es igual al producto de los números en el otro).
Residuo de un factorial (módulo un primo)
Encontrar el residuo que deja 50(50!) al dividirlo entre 53.
Inverso (mod 151) de una potencia de 2
Encontrar un número entero positivo que al multiplicarlo por $2^{145}$ y al resultado restarle 1, se obtenga un múltiplo de 151.
Expresable como combinación lineal
Decidir (con justificación) cuál de los tres números $2007, 2008, 2009$ podría ser expresado como una combinación lineal entera de 453 y 408, es decir, en la forma $453x+408y$, con $x, y$ enteros.
Encontrar un residuo
Encontrar el residuo que deja $2009^{2008}$ al dividirlo entre $9$
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea $ ABC$ un triángulo y sean $ D$, $ E$ y $ F$ los puntos donde la circunferencia circunscrita es tangente al lado $ BC$, $CA$ y $ AB$. Llamemos $D'$ el punto donde la recta $EF$ corta a la recta $AB$. Demuestra que:
a) $D'$ es el conjugado armónico de $D$ con respecto al segmento $ AB$.
b) Que la recta $AD$ es la polar de $D'$ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
Clasificación de primos que dividen a un cuadrado más uno
Demuestra que si $ p$ es un primo impar que divide a $n^2 +1$ para algún $ n$, entonces $ p$ debe ser de la forma $4k+1$, es decir, $p \equiv 1$ (mód 4).
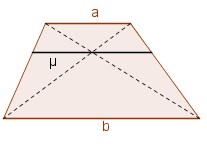
Media armónica de las bases de un trapecio.
Considere $\mu$ un segmento paralelo a las bases $a$ y $b$ de un trapecio, de tal manera que $\mu$ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que $\mu$ es la media armónica de $a$ y $b$, es decir:
No es un cuadrado perfecto
Demostrar que si $y$ es un entero, $187y-1$ no es un cuadrado perfecto.
División anular
Sean $a, b, c$ tres números enteros positivos tales que $a$ divide a $b^2$, $b$ divide a $c^2$ y $c$ divide a $a^2$. Demostrar que $abc$ divide a $a^7+b^7+c^7$.
Tres círculos congruentes
Tres círculos $C_1, C_2, C_3$ del mismo radio se intersectan no tangencialmente en un punto $P$. Sean $A, B$ los centros de $C_1, C_2$, respectivamente; y $C, D$ los puntos de intersección de $C_1, C_2$, respectivamente, con $C_3$. ($C, D$ son ambos diferentes de $P$.) Demostrar que $ABCD$ es un paralelogramo.
