Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Interrupción de la filosofía --en Tijuana
Alejandra (de 37 abriles) fue apañada por un retén de la PGR en Tijuana, el día último de abril, apenas cruzó la aduana procedente de San Diego. Le incautaron 30000 US Dollars, producto de la recaudación por venta de coca en USA.
Una factorización notable (en la IMO 69)
Demuestre que existen infinitos $ m $ enteros positivos tales que $n^4 + m$ es un número compuesto para cualquier $ n $ entero positivo.
Una factorización notable
Encontrar todos los enteros $ n $ tales que $n^4+4$ es primo.
Cíclico en tres circunferencias tangentes
Considere $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$ tres circunferencia que por pares son tangentes externas. Llamemos $P$ y $Q$ los puntos de tangencia de $\mathcal{C}_1$ con $\mathcal{C}_2$ y $\mathcal{C}_3$ respectivamente.
Problema de coolinealidad
Sean $C_1, C_2, C_3$ tres circunferencias tangentes exteriores dos a dos. Definamos los siguientes puntos; $R=C_1 \cap C_2$ $S=C_1 \cap C_3$ y $T=C_2 \cap C_3$ , sean $X, Y$ los puntos sobre $C_2, C_3$ de modo que $XY$ sea la tangente comun y esta no pase por $C_1$. Sea $J$ la interseccion de la tangente a $C_1, C_2$ por $R$ y a la tangente comun a $C_1, C_3$ por $S$.
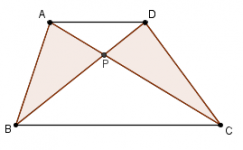
Áreas iguales en un trapecio
Demuestra que para cualquier trapecio ABCD, las áreas de las triángulos sombreados son iguales.
Sumas
Considere las sumas
$$S=4\cdot 5-5\cdot 6 +\ldots - 2009\cdot 2010$$
$$T=3\cdot 6-4\cdot 7+\ldots -2008\cdot 2011$$
Calcular el valor de $S-T$
Producto de diagonales en un polígono regular
Sea $A_1, A_2, \dots, A_n$ los $ n $ vértices de un polígono regular con circunferencia circuncrita de radio $R$, Demuestra que:
Encontrar las soluciones de la igualdad
Encuentre todos los números primos $ p, q $ tales que $ p + q $ = $(p-q)^3$.
Isósceles semejantes sobre un triángulo
Consideremos $A'$, $B'$ y $C'$ tres puntos en el exterior del triángulo $ ABC $, de tal manera que los triángulos $ A'BC $, $ AB'C $ y $ ABC' $ son todos isósceles semejantes y de bases BC, CA y AB respectivamente, Demuestra que $AA'$, $BB'$ y $CC'$ concurren.
Equiláteros en los lados de un triángulo
Este es un problema con la misma figura del triángulo de napoleón.
Consideremos los puntos $A'$, $B'$ y $C'$ puntos fuera del triángulos $ ABC $ de tal manera que los triángulos $ A'BC $, $ AB'C $ y $ ABC' $ son equiláteros. Demuestra que $AA'$, $BB'$ y $CC'$ concurren y son de la misma longitud.
OMM 2008, Problema 6
Las bisectrices internas de los ángulos A, B y C de un triángulo ABC concurren en I y cortan
al circuncírculo de ABC en L, M y N, respectivamente. La circunferencia de diámetro IL,
corta al lado BC, en D y E; la circunferencia de diámetro IM corta al lado CA en F y G;
la circunferencia de diámetro IN corta al lado AB en H y J. Muestra que D, E, F, G, H,
J están sobre una misma circunferencia.
IMO 2008, Problema 1
Un triangulo $ ABC $ tiene ortocentro $ H $. La circunferencia con centro en el punto medio de $ BC $, que pasa por $ H $, corta a la recta $ BC $ en $A_1$y$A_2$, de manera similar se definen los puntos $B_1,B_2$ en la recta $CA$ y $C_1,C_2$ en la recta $AB$. Demuestra que los puntos $A_1, A_2, B_1, B_2, C_1, C_2$ estan en una misma circunferencia.
Una caracterización de los libres de cuadrados
Considera un entero $n > 1$. Demuestra que existen enteros $a,b \geq 1$ tales que $a+b=n$ y $n | ab$ si y sólo si $ n $ no es libre de cuadrados.
Problema básico
Sean $a$ y $b$ dos números enteros positivos tales que $a+b=2009$, probar que 2009 no divide al producto $ab$.
Problema 8 Geometrense
Sean ABC un triángulo y AP, AQ las tangentes desde A a la circunferencia de diámetro BC (P y Q los puntos de tangencia). Muestra que el ortocentro H de ABC está sobre PQ.
Se le quitó la gripa, pero lo porcino... ¿cuándo?
Saliendo del hospital, "Chupy --el muñeco alcoholico--", se detuvo a echarse unos tacos en el carretón de enfrente. Pidió 10 surtidos y una Diet Coke (8 pesos).
Perpendicular si y sólo si el triángulo es isósceles
Sea ABC un triángulo de circuncentro O, sea M el punto medio de AB y E el gravicentro del triángulo AMC. Demostrar que OE y CM son perpendiculares si y sólo si AB=AC
Basico de Algebra
El poder justiciero de los mass media
Al llegar al poder, aquél político y ex-sacerdote, tuvo que reconocer a sus tres hijos ilegítimos ante el inminente escándalo público con que amenazaban sus tres
