XX OMM 2006
P6 OMM 2006. Problema con números surtidos
Sea $n$ la suma de los dígitos de un entero positivo $A$. Decimos que $A$ es “surtido” si cada uno de los enteros $1,2,\ldots,n$ es suma de dígitos de $A$
- Demuestra que si $1,2,\ldots,8$ son sumas de dígitos de un entero $A$ entonces $A$ es surtido.
- Si $1,2,\ldots,7$ son sumas de dígitos de un entero $A$, ¿es $A$ necesariamente surtido?
Nota: El número 117 no es surtido pues sólo $1=1, 2 = 1+1, 7 = 7, 8 = 1 + 7, 9 = 1 + 1 + 7$ se pueden escribir como suma de dígitos de 117.
P5 OMM 2006. Altura de triángulo pedal
Sean $ABC$ un triángulo acutángulo y, $AD, BE$ y $CF$ sus alturas. La circunferencia con diámetro $AD$ corta a los lados $AB$ y $AC$ en $M$ y $N$, respectivamente. Sean $P$ y $Q$ los puntos de intersección de $AD$ con $EF$ y $MN$, respectivamente. Demuestra que $Q$ es el punto medio de $PD$.
P3 OMM 2006. Números 1..2n en cuadrícula 2Xn
Sea $ n $ un número entero mayor que 1. ¿De cuántas formas se pueden acomodar todos los números $1,2,\ldots,2n$ en las casillas de una cuadrícula de $2 \times n$, uno en cada casilla, de manera que cualesquiera dos números consecutivos se encuentren en casillas que comparten un lado de la cuadrícula?
P2 OMM 2006. Semejantes si y sólo si ángulo de 60
Sea $ABC$ un triángulo rectángulo con ángulo recto en $A$, tal que $AB < AC$. Sea $M$ el punto medio de $BC$ y $D$ la intersección de $AC$ con la perpendicular a $BC$ que pasa por $M$. Sea $E$ la intersección de la paralela a $AC$ que pasa por $M$ con la perpendicular a $BD$ que pasa por $B$. Demuestra que los triángulos $AEM$ y $MCA$ son semejantes si y sólo si $\angle ABC = 60°$.
P1 OMM 2006. Los parientes de un número son sus múltiplos
Sea $ab$ un número de dos dígitos. Un entero positivo $ n $ es “pariente” de $ab$ si:
- El dígito de las unidades de $n$ también es $b$.
- Los otros dígitos de $n$ son distintos de cero y suman $a$.
Por ejemplo, los parientes de 31 son 31, 121, 211 y 1111. Encuentra todos los números de dos dígitos que dividen a todos sus parientes .
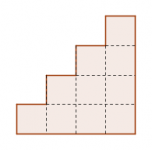
P4 OMM 2006. Zacatecas 2006: n-cubrimiento de una n-escalera
Como se sabe, en problemas de olimpiada, el enunciado puede tener una trampa de significado. El problema 4 del XX concurso nacional de la Olimpiada Mexicana de Matemáticas consiste de una pregunta “para qué enteros…”. La mayoría de los concursantes respondieron a la pregunta. Pero a la hora de las revisiones se supo que no bastaba con decir “estos son” sino que había que demostrar que no había otros. La solución necesitaba estar en el formato “los enteros n cumplen la condición si, y sólo si, son de la forma n = f(k)”. He aquí el enunciado del problema 4 del concurso nacional de 2006.