Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Secuencia de conjuntos no vacios (OMM 2021 P6)
Determina todos los conjuntos no vacíos $C_1, C_2, C_3, \dots$, tales que cada uno de ellos tiene un número finito de elementos y todos sus elementos son enteros positivos, con la siguiente propiedad: Para cualesquiera enteros positivos $m$ y $n$, la cantidad de enteros positivos en el conjunto $C_m$ más la cantidad de enteros positivos en $C_n$ es igual a la suma de los elementos en el conjunto $C_{m+n}$.
Nota: Al denotar con $|C_k|$ la cantidad de elementos de $C_k$ y con $S_k$ la suma de los elementos de $C_k$, la condición del problema es que para $m$ , $n$ enteros positivos se cumple
$$|C_n|+|C_m| = S_{m+n}$$Números digitales (OMM 2021 P5)
Para cada entero $n>0$ con expansión decimal $\overline{a_1a_2 \dots a_k}$ definimos $s(n)$ como sigue:
- Si k es par, $s(n) = \overline{a_1a_2} + \overline{a_3a_4} + \dots +\overline{a_{k-1}a_k} $
- Si k es impar, $s(n) = a_1 + \overline{a_2a_3} + \overline{a_4a_5} + \dots +\overline{a_{k-1}a_k} $
Por ejemplo, si $n=123$ entonces $s(n) = 1 + 23 = 24$ y si $n=2021$ entonces $s(n) = 20+21 = 41$.
Decimos que este $n$ es digital si $n$ es múltiplo de $s(n)$. Muestra que entre cualesquiera 198 enteros positivos consecutivos, todos ellos menores que 2000021, hay uno de ellos que es digital.
Triángulo con ángulo de 60º (OMM 2021 P4)
Sea $ABC$ un triángulo acutángulo escaleno con $\angle BAC = 60 ^\circ$ y ortocentro $H$. Sea $\omega_b$ la circunferencia que pasa por $H$ y es tangente a $AB$ en $B$, y $\omega_c$ la circunferencia que pasa por $H$ y es tangente a $AC$ en $C$.
- Prueba que $\omega_b$ y $\omega_c$ solamente tienen a $H$ como punto común
- Prueba que la recta que pasa por $H$ y el ortocentro $O$ de $ABC$ es tangente común a $\omega_b$ y $\omega_c$
Criterio del 99 (P5 OMM 2021)
La hormiga, el mago y la lava (OMM 2021 P3)
Sean $m,n \geq 2$ dos enteros. En una cuadrícula de $m \times n$, una hormiga empieza en cuadrito inferior izquierdo y quiere camina al cuadradito superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, de acuerdo a las siguientes posibilidades $\uparrow$, $\rightarrow$ y $\nearrow$. Sin embargo, un malvado mago ha dejado caer lava desde arriba y ha destruido algunos cuadritos de forma tal que:
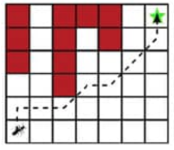
Es punto medio si y sólo si el otro es punto medio (OMM 2021 P2)
Sea $ABC$ un triángulo tal que $\angle ACB > 90^\circ$ y sea $D$ el punto de la recta $BC$ tal que $AD$ es perpendicular a $BC$. Considere $\Gamma$ la circunferencia de diámetro $BC$. Una recta que pasa por $D$ es tangente a la circunferencia $\Gamma$ en $P$, corta al lado $AC$ en $M$ (quedando $M$ entre $A$ y $C$) y corta al lado $AB$ en $N$.
Demuestra que $M$ es punto medio de $DP$ si, y sólo si $N$ es punto medio de $AB$.
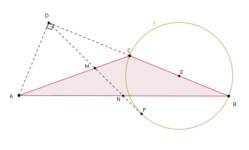
Misma área y lados en progresión arimética (OMM 2021 P1)
Problema 1 - IMO 2019 - Determinar todas las función enteras.
Sea $\mathbb{Z}$ el conjunto de los números enteros. Determinar todas las funciones $f: \mathbb{Z} \to \mathbb{Z}$ tales que, para todos los enteros $a$ y $b$, $$f(2a) + 2f(b) = f (f (a + b)).$$
Demostrar que es equilatero
Sea ABCD un cuadrado.
Se construyen 2 triangulos equilatero hacia afuera, CDE y BCF, se trazan las circunferencia con centro en E y con Centro en F que pasan por CD y BC respectivamente.
Sea P la interseccion de las circunferencias.
Demuestra que el trianguo PDB es equilatero.
Pasa los caballos a las columnas, si puedes...
En un tablero de ajedrez de $2017 \times 2017$, se han colocado en la primera columna 2017 caballos, uno en cada casilla de la columna. Una tirada consiste en elegir dos caballos distintos y de manera simultánea moverlos como se mueven los caballos de ajedrez. Encuentra todos los posibles valores enteros de $k$ con $1\leq k \leq 2017$, para los cuales es posible llegar a través de varias tiradas, a que todos los caballos estén en la columna $k$, uno en cada casilla.
Nota. Un caballo se mueve de una casilla $X$ a una $Y$, solamente si $X$ y $Y$ son las esquinas opuestas de un rectángulo de $3\times 2$ o de $2 \times 3$.
El seis de la ORO. (Paisanos)
Un cambio para un número natural $n$ consiste en agregar una pareja de ceros entre dos dígitos o al final de la representación decimal de $n$. Un paisano de $n$ es un número que se puede obtener haciendo uno o más cambios en $n$. Por ejemplo 40041 y 44001 son paisanos de 441. (Nota: 441 no es paisano de 44100). Determina todos los números naturales $n$ para los cuales existe un número natural $m$ con la propiedad de que $n$ divide a $m$ y a todos los paisanos de $m$.
Tangentes si y sólo si perpendiculares
Sea $ABCD$ un cuadrilátero inscrito en una circunferencia, $l_1$ la recta paralela a $BC$ que pasa por $A$ y $l_2$ la recta paralela a $AD$ que pasa por $B$. La recta $DC$ corta a $l_1$ y $l_2$ en los puntos $E$ y $F$, respectivamente. La recta perpendicular a $l_1$ que pasa por $A$ corta a $BC$ en $P$ y la recta perpendicular a $l_2$ por $B$ corta a $AD$ en $Q$. Sean $\Gamma_1$ y $\Gamma_2$ las circunferencias que pasan por los vértices de los triángulos $ADE$ y $BFC$, respectivamente. Demuestra que $\Gamma_1$ y $\Gamma_2$ son tangentes si y sólo si $DP$ es perpendicular a $CQ$.
Problema clásico con solución atípica
En una cuadrícula de $ n \times n$ se escriben los números del 1 al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.
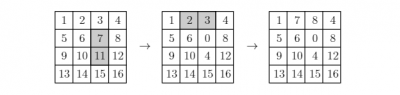
Múltiplo de 7 con dígitos consecutivos
Decimos que un número entero no-negativo $n$ contiene a otro número entero no-negativo $m$, si los dígitos de su expansión (o desarrollo) decimal aparecen en forma consecutiva en la expansión (o desarrollo) decimal de $n$. Por ejemplo 2016 contiene a 2,0,1,6, 20, 16, 201 y 2016. Determina el mayor número entero $n$ que no contiene a ningún múltiplo de 7.
Desigualdades con parte entera
Encuentra el menor número real $x$ que cumpla todas las siguientes desigualdades:
$$ \lfloor x \rfloor < \lfloor x^2 \rfloor < \lfloor x^3 \rfloor < \dots < \lfloor x^n \rfloor < \lfloor x^{n+1} \rfloor < \dots $$
Nota: $\lfloor x \rfloor$ es el mayor entero menor o igual a $x$, es decir, es el único número entero que cumple que $ \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1$.
Parejas Guerreras
Una pareja de enteros positivos $m,n$ es guerrera si existen enteros positivos $a,b,c,d$ con $m=ab, n=cd$ y $a+b=c+d$. Por ejemplo, la pareja 8,9 es guerrera pues $8 = 4 \cdot 2 , 9=3 \cdot 3$ y $4+2=3+3$. Se colorean los enteros positivos de la siguiente manera:
- Empezamos coloreando el 3 y el 5.
- Después , si algún entero positivo no está coloreado y este tiene una pareja guerrera que ya está coloreado, entonces lo coloreamos.
Encuentra todos los enteros positivos que eventualmente se colorean.
Circunferencias con relación de radios
Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ dos circunferencias tangentes externamente en $S$ tales que el radio de $\mathcal{C}_2$ es el triple del radio de $\mathcal{C}_1$. Sea $l$ una recta que es tangente a $\mathcal{C}_1$ en $P$ y tangente a $\mathcal{C}_2$ en $Q$, con $P$ y $Q$ distintos de $S$. Sea $T$ el punto en $\mathcal{C}_2$ tal que $TQ$ es diámetro de $\mathcal{C}_2$ y sea $R$ la intersección de la bisectriz de $\angle SQT$ con el segmento $ST$. Demuestra que $QR = RT$
Números norteños
Un entero positivo $N$ es norteño si para cada dígito $d >0$, existe un divisor de $N$ cuyo último dígito es $d$. ¿Cuántos números norteños menores que 2016 hay que tengan la menor cantidad posible de divisores?
Tercia de reales
Encuentra todas las ternas de reales $(a,b,c)$ tales que $$ a- \frac{1}{b} = b - \frac{1}{c} = c - \frac{1}{a}$$
Punto exterior a un cuadrado
Sea $ABCD$ un cuadrado. P un punto sobre la semicircunferencia de diámetro AB exterior al cuadrado. Sean M y N las intersecciones de PD y PC con AB, respectivamente. Demuestra que $MN^2 = AM \cdot BN$
