Problemas
También puedes compartirnos alguno de tus problemas favoritos:
5.- Borrando divisores de un pizarrón
Sea $n > 1$ un entero positivo y sean $d_1 < d_2 < ... < d_m$ sus $m$ enteros positivos de manera que $d_1 = 1$ y $d_m = n$. Lalo escribe los siguientes $2m$ números en un pizarrón:
$d_1 , d_2 , ... , d_m , d_1 + d_2 , d_2 + d_3 , ... , d_{m-1} + d_m , N$
donde $N$ es un entero positivo. Después Lalo borra los números repetidos (por ejemplo, si un número repetido aparece 2 veces, el borrará uno de los dos). Después de esto, Lalo nota que los números en el pizarrón son precisamente la lista completa de divisores positivos de $N$. Encuentra todos los posibles valores del entero positivo $n$.
4.- También arquitectos
Sea $n$ un entero positivo. En un jardín de $n \times n$ cuyos lados dan al Norte, Sur, Este y Oeste se va a construir una fuente usando plataformas de $1 \times 1$ que cubra todo el jardín.
Ana colocará las plataformas todas a diferente altura. Después, Beto pondrá salidas de agua en algunas de las plataformas.
El agua de cada plataforma puede bajar a las plataformas contiguas (hacia el Norte, Sur, Este y Oeste) que tengan menor altura que la plataforma de donde viene el agua, siguiendo su flujo siempre que pueda dirigirse a plataformas de menor altura. El objetivo de Beto es que el agua llegue a todas las plataformas.
3.- Orquesta Matemática
Sea $n>1$ un entero y sea $d_1 < d_2 < \dots < d_m$ la lista completa de sus divisiores positivos, incluidos $1$ y $n$. Los $m$ instrumentos de una orquesta matemática se disponen a tocar una pieza musical de $m$ segundos, donde el instrumento $i$ tocará una nota de tono $d_i$ durante $s_i$ segundos (no necesariamente consecutivos), donde $d_i$ y $s_i$ son enteros positivos. Decimos que esta pieza tiene sonoridad $S = s_1 + s_2 + \cdots + s_m $.
2.- Ataque de torres en un tablero cúbico.
Sea $n$ un entero positivo. David tiene 6 tableros de ajedrez de $n \times n$ que ha dispuesto de manera que formen las 6 caras de un cubo de $n \times n \times n$. Se dice que dos casillas $a$ y $b$ de este nuevo tablero cúbico están alineadas si podemos conectarlas por medio de un camino de casillas $a = c_1, c_2, \dots, c_m = b$ de manera que cada pareja de casillas consecutivas en el camino comparten un lado, y los lados que la casilla $c_i$ comparte con sus vecinas son lados opuestos del cuadrado $c_i$, para $i = 2, 3, \dots, m-1$. Diremos que dos torres colocadas sobre el tablero se atacan; si las casillas que ocupan están alineadas. David coloca algunas torres sobre el tablero de forma que ninguna ataque a otra.
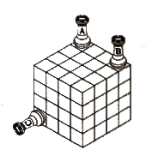
1.- Números Tlahuicas
Un número $x$ es Tlahuica si existen números primos distintos $p_1, p_2 \dots, p_k$ tales que
$$x= \frac{1}{p_1} + \frac{1}{p_2} + ... + \frac{1}{p_k}$$Determina el mayor número Tlahuica que satisface las dos propiedades siguientes:
- 0 < x < 1
- existe un número entero $0 < m \leq 2022$ tal que $mx$ es un entero.
El 6 del último selectivo 2022
Se definen las sucesiones xn y yn mediante las siguientes reglas:
- x0 = 2, x1 = 5, xn+1 = xn + 2xn-1
- y0 = 3, y1 = 4, yn+1 = yn + 2yn-1
Demuestra que no hay números que estén en ambas sucesiones.
Sin miedo al factorial
Determina el menor entero positivo $n$ tal que para todo entero positivo $u$ se cumple que $n+u!$ sea un número de al menos 4 divisores
Isósceles en 2 circunferencias de mismo radio
Sean $\alpha$ y $\beta$ dos circunferencias con el mismo radio. Dichas circunferencias se intersectan en puntos$P$ y $Q$. Sea $X$ un punto en $\alpha$. La recta $QX$ intersecta a $\beta$ en un punto $Z$, de manera que $Z$ queda entre $X$ y $Q$. Demuestra que $PX=PZ$.
Paralelogramo con solo 3 vértices en una circunferencia
Sea $ABCD$ un paralelogramo. Sean $K$ y $L$ las intersecciones del circuncírculo de $ABC$ con los lados $AD$ y $CD$ respectivamente. Sea $M$ el punto medio del arco $KL$ que no contiene a $B$. Demuestra que $DM$ es perpendicular a $AC$.
Múltiplos de 9 con restricciones
¿Cuántos múltiplos de 9 menores que 1000 no usan ningún digito menor que 3?
Promedio de un colección de m números
a) Demuestra que si a una colección de $m$ números le agregamos su promedio, la nueva colección de $m+1$ números tendrá el mismo promedio.
b) Demuestra que el promedio de una colección de m números es menor o igual a su número más grande, y mayor o igual a su número más pequeño.
EXTRA PARA ENTRENAMIENTO:
c) Demuestra que si a la colección le agregamos un número menor al promedio, entonces el promedio disminuye. En cambio, si agregamos un número mayor al promedio, entonces el promedio aumenta.
El 6 del estatal 2022
En una circunferencia $\Gamma$ con centro en $D$ se trazan dos tangentes $AE$ y $AF$ con $E$ y $F$ sobre $\Gamma$. Sean $B$ y $C$ puntos sobre los segmentos $AE$ y $AF$ respectivamente de tal manera que $BC$ también es tangente a $\Gamma$. Sea $J$ la intersección de $BD$ con $EF$. Demuestra que el ángulo $CJB$ es un ángulo recto.
Problema 5 Estatal 2022
Encuentra todas las parejas de enteros positivos (x,n) tales que:
(3)(2x) + 4 = n2
Matrimonios en una mesa
A una cena llegan 3 matrimonios. Se quieren sentar alrededor de una mesa redonda de manera que nadie quede junto a su pareja. ¿De cuántas formas se pueden acomodar si Ana ya tiene un lugar asignado fijo?
El 3 del estatal 2022
Encuentra todos los valores para n de tal forma que la expresión
6n+1
sea un número con todos sus dígitos iguales.
Juego con una bolsa de 2022 piedras
Julieta y Edwin juegan al siguiente juego. Se empieza con una bolsa que contiene 2022 piedras. Se juega por turnos alternados y cada jugador puede hacer lo siguiente:
- Si el número de piedras en la bolsa es par, el jugador puede tomar una piedra o la mitad de las piedras.
- Si el número de la bolsa es impar, tiene que tomar una sola piedra.
Gana quien tome la última piedra. Julieta empieza el juego.
Determina quién tiene una estrategia ganadora y explícala.
Mesa hexagonal con mantel rectangular
Carlos tiene una mesa en forma de hexágono regular y un mantel rectangular con área 2022 que cubre un rectángulo de la mesa formado por exactamente dos lados paralelos de la mesa como bases del rectángulo. ¿Cuál es el área de la mesa?
El difícil de la segunda ronda (el 4)
Tenemos 16 mosaicos que tienen dos cuartos de circunferencia centradas en esquinas opuestas cuyo radio es la mitad del lado de la baldosa como se muestra:
Pon a prueba tu vista
En el trapecio ABCD de bases AB y CD, las diagonales AC y BD son perpendiculares entre sí. Los Segmentos AB y BD miden 20 m y 17 m respectivamente. El área del triángulo ABD es 102 m2. ¿Cuántos metros mide el lado CD?
El número de Belmaris
André, Belmaris, Claudia, Daniel, Elmer y Germán van a jugar a decir números en ese orden. André y Belmaris podrán elegir sus números, pero los siguientes deben decir el resultado de la multiplicación de los números que dijeron las dos personas antes que ellos, sin equivocarse. Si André dijo "2" y Germán dijo "6 075 000" (seis millones setenta y cinco mil), ¿qué numero dijo Belmaris?
