Problemas
También puedes compartirnos alguno de tus problemas favoritos:
P5 Concurrencia de 2 círculos y 1 segmento
Sean $ABC$ un triángulo acutángulo, $\Gamma$ su circuncírculo y $O$ su circuncentro. Sea $F$ el punto en $AC$ tal que $\angle COF = \angle ACB$, donde $F$ y $B$ están de lados opuestos respecto a $CO$. La recta $FO$ corta a $BC$ en $G$. La paralela a $BC$ por $A$ interseca a $\Gamma$ de nuevo en $M$. Las rectas $MG$ y $CO$ se cortan en $K$. Demuestra que los circuncírculos de los triángulos $BGK$ y $AOK$ concurren en $AB$.
P3 Regresa la Geo a la OMM
Sea $ABCD$ un cuadrilátero convexo. Si $M, N, K$ son los puntos medios de los segmentos $AB$, $BC$ y $CD$ respectivamente, y además existe un punto $P$ dentro del cuadrilátero $ABCD$ tal que, $\angle BPN = \angle PAD$ y $\angle CPN = \angle PDA$. Demuestra que $AB \cdot CD$ = $4PM \cdot PK$
3.- Ortocentro como Punto Medio
Sean $ABC$ un triángulo acutángulo, $H$ su ortocentro y $M$ el punto medio de $BC$. La perpendicular a $MH$ por $H$ corta a $AB$ en $L$ y a $AC$ en $N$. Demuestra que $LH=HN$.
NOTA: El ortocentro es la intersección de las alturas del triáungulo.
Un triángulo acutángulo es aquel que tiene sus 3 ángulos agudos.
6.- 480°???
Sea $ABC$ un triángulo equilátero. Sean $A_1$, $B_1$ y $C_1$ puntos interiores de $ABC$ tales que $BA_1$ = $A_1C$, $CB_1$ = $B_1A$, $AC_1$ = $C_1B$ y <$BA_1C$ + <$CB_1A$ + <$AC_1B$ = 480°.
Las rectas $BC_1$ y $CB_1$ se cortan en $A_2$, las rectas $CA_1$ y $AC_1$ se cortan en $B_2$, y las rectas $AB_1$ y $BA_1$ se cortan en $C_2$.
Demuestra que si el triángulo $A_1B_1C_1$ es escaleno, entonces los tres circuncírculos de los triángulos $AA_1A_2$, $BB_1B_2$ y $CC_1C_2$ pasan todos por dos puntos comunes.
NOTA: un triángulo escaleno tiene sus 3 longitudes de lados distintos.
2.- Revive la geo con una concurrencia
Sea $ABC$ un triángulo acutángulo con $AB < AC$. Sea Ω el circuncírculo de ABC. Sea S el punto medio del arco $CB$ de Ω que contiene a A. La perpendicular por $A$ por $BC$ corta al segmento $BS$ en $D$ y a Ω de nuevo en E ≠ A. La paralela a $BC$ por $D$ corta a la recta $BE$ en $L$. Sea ω el circuncírculo del triángulo $BDL$. Las circunferencias ω y Ω se cortan de nuevo en P ≠ B. Demuestra que la recta tangente a ω en P corta a la recta BS en un punto de la bisectriz interior del ángulo <$BAC$.
P8. Hexágonos de palitos con áreas iguales
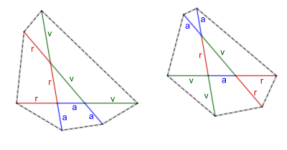
Se tienen nueve palitos de madera: tres azules de longitud $a$ cada uno, tres rojos de longitud $r$ cada uno y tres verdes de longitud $v$ cada uno, tales que es posible formar un triángulo $T$ con palitos de colores distintos.
Dana puede formar dos arreglos, comenzando con $T$ y utilizando los otros seis palitos para prolongar los lados de $T$, como se muestra en la figura. De esta manera se pueden formar dos hexágonos cuyos vértices son los extremos de dichos seis palitos. Demuestra que ambos hexágonos tienen la misma área.
P2. Matilda dibuja cuadriláteros
Matilda dibuja 12 cuadriláteros. El primer cuadrilátero que dibuja es un rectángulo de lados enteros y 7 veces más ancho que alto. Cada vez que termina de dibujar un cuadrilátero, une los puntos medios de cada pareja de lados consecutivos con segmentos de recta para así obtener el siguiente cuadrilátero. Se sabe que el último cuadrilátero que dibuja Matilda es el primero en tener área menor a 1. ¿Cuál es el área máxima posible del primer cuadrilátero?

6.- Punto ideal de semejanza
Encuentra todos los $n \geq 3$, tales que existe un polígon convexo de $n$ lados $A_1A_2 \dots A_n$, que tenga las siguientes características:
- todos los ángulos internos de $A_1A_2 \dots A_n$ son iguales
- no todos los lados de $A_1A_2 \dots A_n$ son iguales
- existe un triángulo $T$ y un punto $O$ en el interior de $A_1A_2 \dots A_n$ tal que los $n$ triángulos $OA_1A_2$, $OA_2A_3$, $\dots$, $OA_{n-1}A_n$ son todos semejantes a $T$
NOTAS:
Isósceles en 2 circunferencias de mismo radio
Sean $\alpha$ y $\beta$ dos circunferencias con el mismo radio. Dichas circunferencias se intersectan en puntos$P$ y $Q$. Sea $X$ un punto en $\alpha$. La recta $QX$ intersecta a $\beta$ en un punto $Z$, de manera que $Z$ queda entre $X$ y $Q$. Demuestra que $PX=PZ$.
Paralelogramo con solo 3 vértices en una circunferencia
Sea $ABCD$ un paralelogramo. Sean $K$ y $L$ las intersecciones del circuncírculo de $ABC$ con los lados $AD$ y $CD$ respectivamente. Sea $M$ el punto medio del arco $KL$ que no contiene a $B$. Demuestra que $DM$ es perpendicular a $AC$.
El 6 del estatal 2022
En una circunferencia $\Gamma$ con centro en $D$ se trazan dos tangentes $AE$ y $AF$ con $E$ y $F$ sobre $\Gamma$. Sean $B$ y $C$ puntos sobre los segmentos $AE$ y $AF$ respectivamente de tal manera que $BC$ también es tangente a $\Gamma$. Sea $J$ la intersección de $BD$ con $EF$. Demuestra que el ángulo $CJB$ es un ángulo recto.
Mesa hexagonal con mantel rectangular
Carlos tiene una mesa en forma de hexágono regular y un mantel rectangular con área 2022 que cubre un rectángulo de la mesa formado por exactamente dos lados paralelos de la mesa como bases del rectángulo. ¿Cuál es el área de la mesa?
Pon a prueba tu vista
En el trapecio ABCD de bases AB y CD, las diagonales AC y BD son perpendiculares entre sí. Los Segmentos AB y BD miden 20 m y 17 m respectivamente. El área del triángulo ABD es 102 m2. ¿Cuántos metros mide el lado CD?
Problema 3. 21a OMM Final Estatal
En la figura, $ABC$ es un triángulo isósceles con $|AB| = |AC|$; $D$ es un punto sobre $AC$ tal que $DB$ es perpendicular a $BC$; $E$ es un punto sobre la recta $BC$ tal que $|CE| = 2|BC|$ y $F$ es un punto sobre $ED$ tal que $FC$ es paralela a $AB$. Probar que la recta $FA$ es paralela a $BC$.
Problema 4 - IMO 2022 - Un cíclico a partir de un pentágono
Hexágono dentro de triángulos equilateros.
La siguiente figura está formada por 6 triángulos iguales de lado igual al doble del lado del hexágono central. ¿Qué fracción de la figura completa representa el hexágono central?

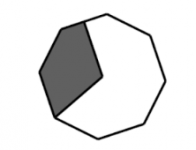
Uno imposible de un octágono
El área total del siguiente octágono es de 2022 cm2, ¿cuál es el área de la región sombreada?
Suelo con mosaicos
Un suelo se va a llenar con mosaicos como el siguiente, formado por mosaicos cafés más pequeños como los mostrados en la figura. El área blanca se llenará con mosaicos azules del mismo tamaño que el café. Al llenarse todo el suelo se utilizaron 192 cafés, ¿cuántos mosaicos azules fueron necesarios?

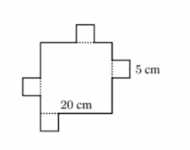
Halla el perímetro
Sobre los lados de un cuadrado de 20 x 20 cm se dibujan cuadrados de 5 x 5 cm como se muestra en la figura. ¿Cuál es el perímetro de la siguiente figura?
Triángulo con ángulo de 60º (OMM 2021 P4)
Sea $ABC$ un triángulo acutángulo escaleno con $\angle BAC = 60 ^\circ$ y ortocentro $H$. Sea $\omega_b$ la circunferencia que pasa por $H$ y es tangente a $AB$ en $B$, y $\omega_c$ la circunferencia que pasa por $H$ y es tangente a $AC$ en $C$.
- Prueba que $\omega_b$ y $\omega_c$ solamente tienen a $H$ como punto común
- Prueba que la recta que pasa por $H$ y el ortocentro $O$ de $ABC$ es tangente común a $\omega_b$ y $\omega_c$
