Problemas

Sean $ABC$ un triángulo acutángulo, $H$ su ortocentro y $M$ el punto medio de $BC$. La perpendicular a $MH$ por $H$ corta a $AB$ en $L$ y a $AC$ en $N$. Demuestra que $LH=HN$.

NOTA: El ortocentro es la intersección de las alturas del triáungulo. 

Un triángulo acutángulo es aquel que tiene sus 3 ángulos agudos.

Determina todas las parejas de enteros positivos $(p, k)$ con $p$ un número primo tales que:

$p^k-k^p=9k$

Sea $ABC$ un triángulo equilátero. Sean $A_1$, $B_1$ y $C_1$ puntos interiores de $ABC$ tales que $BA_1$ = $A_1C$, $CB_1$ = $B_1A$, $AC_1$ = $C_1B$ y <$BA_1C$ + <$CB_1A$ + <$AC_1B$ = 480°. 

Las rectas $BC_1$ y $CB_1$ se cortan en $A_2$, las rectas $CA_1$ y $AC_1$ se cortan en $B_2$, y las rectas $AB_1$ y $BA_1$ se cortan en $C_2$. 

Demuestra que si el triángulo $A_1B_1C_1$ es escaleno, entonces los tres circuncírculos de los triángulos $AA_1A_2$, $BB_1B_2$ y $CC_1C_2$ pasan todos por dos puntos comunes. 

NOTA: un triángulo escaleno tiene sus 3 longitudes de lados distintos.

Sean $x_1$, $x_2$, ..., $x_{2023}$ números reales positivos, todos distintos entre sí, tales que

$a_n$ = $\sqrt{(x_1 + x_2 + ... + x_n)(\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n})}$
 

es entero para todo $n$ = 1, 2, ..., 2023. Demuestra que $a_{2023} \geq 3034$.

Sea $ABC$ un triángulo acutángulo con $AB < AC$. Sea Ω el circuncírculo de ABC. Sea S el punto medio del arco $CB$ de Ω que contiene a A. La perpendicular por $A$ por $BC$ corta al segmento $BS$ en $D$ y a Ω de nuevo en E ≠ A. La paralela a $BC$ por $D$ corta a la recta $BE$ en $L$. Sea ω el circuncírculo del triángulo $BDL$. Las circunferencias ω y Ω se cortan de nuevo en P ≠ B. Demuestra que la recta tangente a ω en P corta a la recta BS en un punto de la bisectriz interior del ángulo <$BAC$.

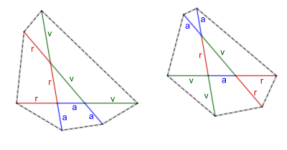
Se tienen nueve palitos de madera: tres azules de longitud $a$ cada uno, tres rojos de longitud $r$ cada uno y tres verdes de longitud $v$ cada uno, tales que es posible formar un triángulo $T$ con palitos de colores distintos.

Dana puede formar dos arreglos, comenzando con $T$ y utilizando los otros seis palitos para prolongar los lados de $T$, como se muestra en la figura. De esta manera se pueden formar dos hexágonos cuyos vértices son los extremos de dichos seis palitos. Demuestra que ambos hexágonos tienen la misma área.

Alka encuentra escrito en un pizarrón un número $n$ que termina en 5. Realiza una secuencia de operaciones con el número en el pizarrón. En cada paso decide realizar una de las dos operaciones siguientes:

1. Borrar el número escrito $m$ y escribir su cubo $m^3$.
2. Borrar el número escrito $m$ y escribir el producto $2023\cdot m$

Alka realiza cada una de las operaciones un número par de veces en algún orden y al menos una vez, y obtiene finalmente el número $r$. Si las cifras de las decenas de $r$ es un número impar, encuentra todos los valores posibles que la cifra de las decenas de $n^3$ pudo haber tenido.

Se tiene un función $g$ tal que para todo entero $n$: \[ g(n) = \begin{cases} 1 &\quad \textrm{si } n \geq 1 \\ 0& \quad \textrm{si } n \leq 0 \end{cases} \] También se tiene la función $f$ que cumple lo siguiente para todos los enteros $n \geq 0$ y $m \geq 0$: \[f(0,m) =0 \quad \textrm{y}\] \[f(n+1, m) = \Big( 1 -g(m) + g(m) \cdot g\big(m-1 - f(n,m)\big) \Big)\Big(1+ f(n,m) \Big)\] Encuentra todas las posibles funciones $f$ que cumplen estas condiciones. Es decir, encuentra todas las asignaciones $f(m,n)$ que cumplan las propiedades de arriba para todos los enteros $n \geq 0$ y $m \geq 0$.

Matilda dibuja 12 cuadriláteros. El primer cuadrilátero que dibuja es un rectángulo de lados enteros y 7 veces más ancho que alto. Cada vez que termina de dibujar un cuadrilátero, une los puntos medios de cada pareja de lados consecutivos con segmentos de recta para así obtener el siguiente cuadrilátero. Se sabe que el último cuadrilátero que dibuja Matilda es el primero en tener área menor a 1. ¿Cuál es el área máxima posible del primer cuadrilátero?